| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- shrinkmatch paper
- dann paper
- remixmatch paper
- BYOL
- dcgan
- ConMatch
- WGAN
- tent paper
- mocov3
- CoMatch
- semi supervised learnin 가정
- conjugate pseudo label paper
- Meta Pseudo Labels
- 백준 알고리즘
- UnderstandingDeepLearning
- cifar100-c
- shrinkmatch
- 최린컴퓨터구조
- adamatch paper
- CycleGAN
- SSL
- GAN
- mme paper
- Pseudo Label
- 딥러닝손실함수
- 컴퓨터구조
- Entropy Minimization
- Pix2Pix
- CGAN
- simclrv2
- Today
- Total
Hello Computer Vision
비전공생의 SAM(2021) 논문 리뷰 본문
논문의 풀 제목은 Sharpness-Aware minimization for efficient improving generalization이다.
https://openreview.net/pdf?id=6Tm1mposlrM
Introduction
많은 머신러닝 모델들이 general하게 훈련되어야 하지만 사실은 오버피팅 된다고 한다. 그러므로 training set을 넘어서 generalize하게 만드는 procedure가 필수적이라고 언급한다. 아쉽게도 일반적으로 사용되는 손실함수들은(e.g., cross-entropy) generalization하기에는 충분하지 않다고 한다(항상 상기해야할 부분은 우리는 training 데이터셋에 대해서 손실함수를 최소로 하는 것이 목적이 아니라 Real world data의 sampling이라 할 수 있는 Test 데이터에 대해 손실함수를 최소로 해야한다. 그러기 위한 1차 목표가 training dataset에 대한 손실값을 줄이는 것이긴 하지만 여기서 언급하는 부분은 최근 최적화 방법들은 training dataset에 대해 손실함수를 낮춰도 일반화가 잘 되지않는 것에 대해 지적하고 있는 것이다). 이것에 대해서는 training loss landscape가 commonly complex, non convex하다고 표현한다(non convex: local minima가 다수 존재하므로 초기 파라미터가 어디서 시작하냐에 따라 수렴하는 위치가 달라진다). 추가적으로 지적한 부분은 global, localminima 가 많이 있어 어디로 수렴하냐에 따라 일반화 성능 차이가 나는 것도 지적한다.

위 이미지는 논문에서 나온 이미지인데 왼쪽이 SGD를 이용해 ResNet을 훈련하는 것을 시각화한 것인데 매우 복잡하고 minimum으로 가기위해서는 굉장히 어려워보이지만 오른쪽은 SAM을 이용해 훈련했을 때 complex하지 않은 것을 확인할 수 있다. 따라서 옵티마이저를 선정하는 것은 중요한 것이라고 말을 한다(e.g., Adam, SGD, RMSProp). 추가적으로 training process를 개선하기 위한 방법들이 있는데 BN, data augmentation, dropout, mixed sample augmentation, stochastic depth가 이에 해당된다.
loss landscape, generalization의 연관성에 대해서는 많은 연구가 이루어졌고 두개의 연관성은 분명하다고 한다. 그러나 이러한 문제점들을 개선한 모델을 찾기 굉장히 힘들었다고 한다. 따라서 저자는 novel procedure을 소개한다. 해당 논문에서의 contribution은 다음과 같다(해당 landscape, generalization에 대한 연구는 https://arxiv.org/abs/1609.04836 해당 논문에서 설명되어있다. 결과적으로 말하자면 sharp minima를 찾았을 때와 flat minima를 찾았을 때를 비교하자면 flat minima를 찾았을 때 일반화를 더 잘한다고 한다).
1. Sharpness-Aware Minimization 소개. Generalization, simultaneously minimizing loss value, loss sharpness.
2. CIFAR10, 100, ImageNet 등 많은 CV task에 적용.
3. SAM이 label noise에 대해 robustness 제공
4. loss sharpness, generalization과의 연관성 설명
Sharpness-Aware Minimization(SAM)
우리의 목표는 S라는 데이터를 보고 low population loss(여기서는 L_d(w)라고 표시된다)를 만드는 모델 파라미터 w를 찾는 것이 목적이다. 이러한 목적을 이루기 위해서는(minimizing population loss) S 데이터셋에 대한 loss를 활용하고 풀어야한다. 그러나 최신 딥러닝의 최적화 방법은 test시 suboptimal만 찾게된다(아마 기존 손실함수가 complex, non convex 하기 때문에 optimal찾기 힘들고 local minima에 빠지는 말과 동치인 거 같다). 그래서 저자는 sharpness, loss landscape과의 connection에 주목하여, training loss를 줄이는 것에 집중하는 것이 아니라 entire neighborhoods도 low loss를 갖게하는 파라미터를 찾는다고 한다(결국 이 말은 flat minima를 찾겠다고 선언한 것과 같다).

여기서 p는 0보다 큰 수이고 이러한 수식을 만족한다면 좌변에 있는 population loss가 낮아질 것이라 보는 거 같다(근데 왜 Max로 되어있는지는 처음에 이해를 잘 못했지만 천천히 계속 보면은 아래에서 결국 최소화하는 식이다). 우변의 식들을 다시 쓰면 밑의 식과 같다.

잘 보면 L_s 를 더하고 뺀 것을 알 수 있는데 이것을 괄호로 다시 묶은 것을 확인할 수 있다. 첫번째 [max L_s - L_s] 는 L_s식의 sharpness 를 나타낸다고 한다. 설명해보자면 w에 의한 L_s가 w -> w+ e 로 증가했을 때얼마나 빨리 증가하는지를 나타낸다. 그리고 L_s는 데이터셋에 대한 손실함수를 나타내고 h는 단조증가함수이고 h(||w||)는 L2 정규화를 나타낸다. 그래서 최종적으로는 저자는 해당 밑의 수식을 풀려고 노력한다. 위 수식에 대해 조금 더 개인적인 해석을 넣어보자면 우리는 sharpness를 최대로 하는 epsilon을 찾으면서 결과적으로 전체 손실함수가 작아지는 쪽으로 훈련을 진행한다. 다음 상황 예시를 들어 한번 이해한 것을 써보자면,
1. parameter w가 훈련을 하면서 sharp minima를 찾았다. 그러나 sharp minima는 sharpness가 크기 때문에 손실함수가 크게 형성되며 따라서 파라미터는 다른 곳으로 이동한다.
2. flat minima를 찾았다면 sharpness 가 줄어들 것이고 전체 손실함수가 적어질 것이므로 해당 근처로 수렴한다.

해당 수식을 최적화했을 때 위에서 보여준 이미지처럼 SAM방식은 sharp minimum으로 수렴하는 것을 막는다고 한다. 결국 이 식을 다시 써보자면 $Min [max_{\epsilon} L_{S}^ (w + \epsilon) $ 으로 이해한 바로는 L을 최대화하는 perturbation $\epsilon $을 찾고 최종적인 L_SAM을 최소화하는 것이 최종목표라고 볼 수 있다(약간 헷갈림..).
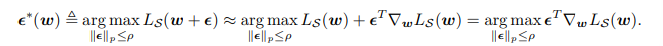
0과 매우 근접한 $\epsilon$에 대해 1차 테일러 급수를 활용하여 위와 같이 변형할 수있다고 한다. 그리고 $\epsilon$에 대해 L를 최대화 하는 것에 대해 L(w)는 관련이 없으니 제외해주는 모습을 위 식에서 볼 수 있다. 위 식은 dual norm problem 으로 인해 아래 식으로 근사할 수 있다고 한다. Appendix 에 이 내용이 서술되있다고 하나 딥하게는 안들어가려고 한다. 결국 위 식은 내가 찾은 minima값이 sharp / flat인지 판단 위한 epsilon값을 찾는 것이다(지극히 개인적인 이해를 위한 해석).


많이 헷갈리기도 하니 pseudo code바탕으로 차례차례보면은 조금 이해가 쉽다(각 선이 가까우면 기울기가 가파른 것이다). pseudo code에서 나온 equation 2는 위의 epsilon을 근사한 식이고 말로 식 대신 말로 써보자면 parameter w에 대해 sharpness가 되는 epsilon값을 찾는 것이라고 보면 된다.
우리가 기본적으로 하는 방식은 w_t에 대해 w_t+1(우상향하는 주황색 화살표)방향으로 학습하는 것이 기본이라고 할 수 있다. 그러나 여기서는 먼저 기존 파라미터 w에서 Loss를 최대화시키도록 하는 perturbation, 즉 0에 근사하는 $\epsilon$을 구한 후 Loss를 최소화하는 gradient를 구해준다. 그리고 이 gradient에 대해서 기존 w_t에 대해 빼주면 되는 것이다.
Empirical Evaluation

'딥러닝' 카테고리의 다른 글
| UnderstandingDeepLearning-Shallow neural networks (0) | 2023.09.20 |
|---|---|
| Understanding DeepLearning-Supervised learning (0) | 2023.09.19 |
| torch.topk 함수 공부해보기 (1) | 2023.08.22 |
| np.random.choice 공부해보기 (0) | 2023.08.21 |
| Test Time Augmentation 알아보기 (0) | 2023.07.10 |


