| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- shrinkmatch paper
- Pix2Pix
- CoMatch
- dann paper
- simclrv2
- tent paper
- 백준 알고리즘
- SSL
- semi supervised learnin 가정
- UnderstandingDeepLearning
- shrinkmatch
- mme paper
- CGAN
- 최린컴퓨터구조
- dcgan
- Entropy Minimization
- BYOL
- 컴퓨터구조
- remixmatch paper
- mocov3
- CycleGAN
- Pseudo Label
- GAN
- conjugate pseudo label paper
- Meta Pseudo Labels
- WGAN
- 딥러닝손실함수
- cifar100-c
- ConMatch
- adamatch paper
- Today
- Total
Hello Data
UnderstandingDeepLearning-Shallow neural networks 본문
1. Neural Network example
Shallow neural networks 는 다음과 같은 함수로 나타날 수 있다. $ y= f[x, \phi] $ 여기서 $ \phi $는 multivariate x에 대해 multivariate y에 대해 mapping하는 파라미터이다.
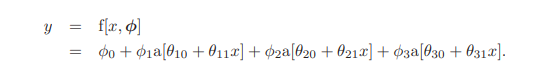
여기서 a는 activation function이다. 가장 흔한 ReLU를 적용하면 다음과 같이 적용된다. relu를 통해 [0, 양수]로 clipping하는 효과가 있다.
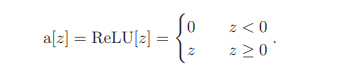
이러한 방식을 통해 model을 훈련하고 Loss를 최적화하는 parameter $\phi^{hat} $을 찾을 수 있다.
3-1식을 조금 간단하게 써보면 다음과 같다.
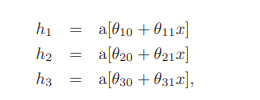
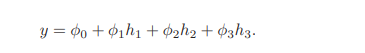
여기서 h를 hidden units라고 칭한다. 3개의 clipped line은 $\phi_{1,2,3} $에 의해 가중치가 정해진다. 이를 한번 시각화해보면 다음과 같다.
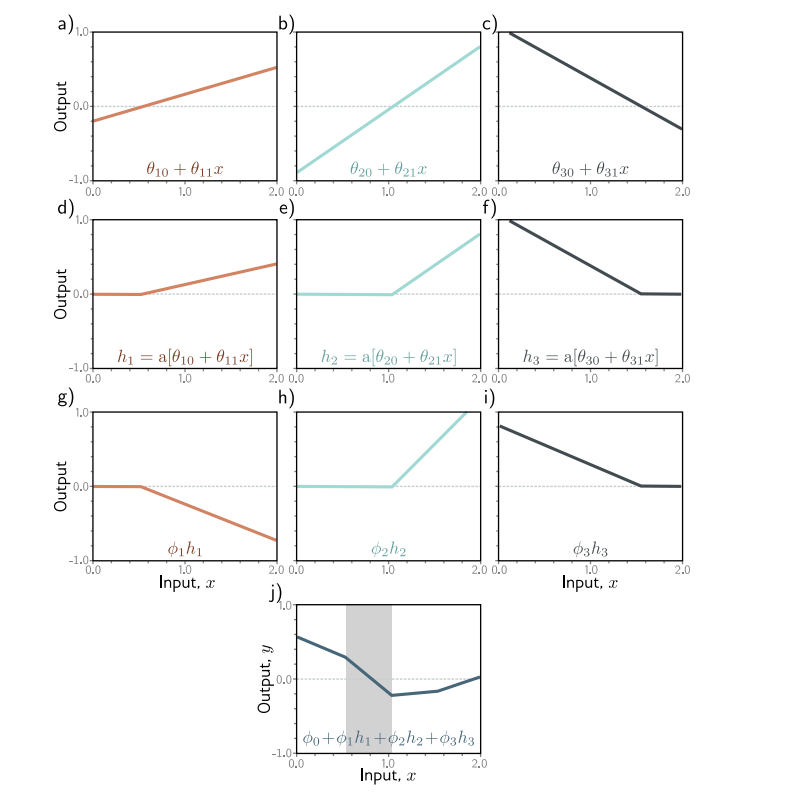
이를 조금 더 우리가 익숙한 neural network로 표현하면 다음과 같다.

2. Universal approximation theorem
위에서는 하나의 input에 대하여 하나의 output을 내뱉고 3개의 hidden units를 가지는 간단한 neural network였다면, D개의 hidden unit을 가지는 neural network는 다음과 같이 일반화할 수 있다.


위에서 neural network의 3개 hidden units로 인해 만든 함수가 있다면 D개의 hidden units가 있다면 D+1개의 linear regions가 만들어지므로 조금 더 복잡한 함수가 된다(여기서 D+1인 이유는 아마 bias이지 않을까 생각한다).
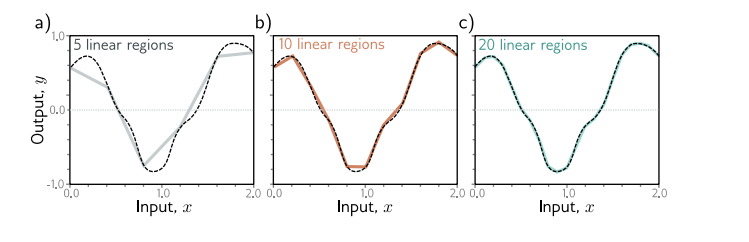
universal approximation theorem 에서 증명한 바에 따르면, 충분한 hidden units가 있다면 shallow neural network는 어떠한 continuous function을 표현할 수 있다고 한다.
universal approximation theorem 은 1개의input, output에만 적용되는 것이 아니라 다변량 x, y에 대해서도 적용이 된다고 한다. 이를 시각화해보면 다음과 같다.
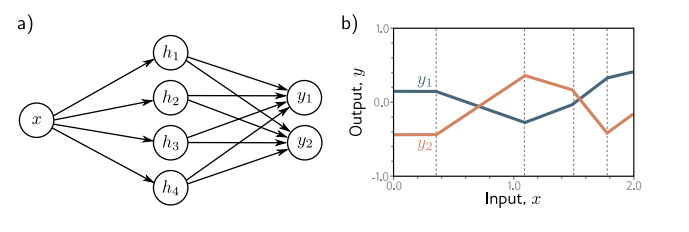
1개의 input에 대해 4 hidden units, 2개의 결과를 갖는 neural network이다. 조금 더 일반화된 시각화를 가져오면 다음과 같다.
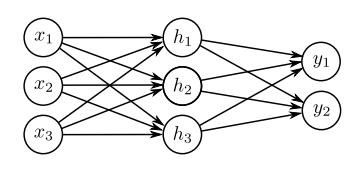
여기서 activation function은 모델로 하여금 x-y mapping을 non-linear하도록 돕는다.
'딥러닝' 카테고리의 다른 글
| 비전공생의 GradNorm(2018) 논문리뷰 (0) | 2023.12.14 |
|---|---|
| UnderstandingDeepLearning-Deep neural networks (0) | 2023.09.20 |
| Understanding DeepLearning-Supervised learning (0) | 2023.09.19 |
| 비전공생의 SAM(2021) 논문 리뷰 (0) | 2023.09.19 |
| torch.topk 함수 공부해보기 (1) | 2023.08.22 |




