| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- Pix2Pix
- cifar100-c
- semi supervised learnin 가정
- 최린컴퓨터구조
- WGAN
- CycleGAN
- mocov3
- tent paper
- simclrv2
- dann paper
- CGAN
- 백준 알고리즘
- mme paper
- shrinkmatch
- dcgan
- ConMatch
- shrinkmatch paper
- 컴퓨터구조
- remixmatch paper
- GAN
- Entropy Minimization
- CoMatch
- conjugate pseudo label paper
- 딥러닝손실함수
- SSL
- adamatch paper
- Pseudo Label
- Meta Pseudo Labels
- BYOL
- UnderstandingDeepLearning
- Today
- Total
Hello Computer Vision
마할라노비스 거리 공부해보기 본문
해당 내용은 아래의 블로그들을 참고해 작성하였습니다.
https://angeloyeo.github.io/2022/09/28/Mahalanobis_distance.html
https://darkpgmr.tistory.com/41
현재 OOD detection공부를 하고 있는데 대표적인 논문 중 하나가 score function을 마할라노비스로 정의하기도 하고 이렇게 정의하는 것이 좋은지 최근 논문도 이렇게 사용하고 있다. 기존에도 데이터의 분포를 고려한 거리지표라는 건 어느 정도 알고 있었는데 이번에 한번 알아보려고 한다.
2차원 좌표에서 x, y 두 점 사이의 거리를 유클라디안 거리로 표현해보자면 다음과 같다.
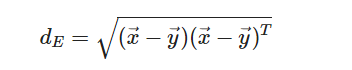
그러나 해당 수치는 데이터의 분포를 고려하지 못하는데 아래 이미지를 보면 딱 이해할 수 있다.

a, b라는 두개의 데이터 분포를 얻었다고 생각해보자. 두 점 x, y의 거리를 유클라디안 거리로 계산해본다면 같다는 것을 알 수 있다. 그러나 과연 이 두 점 사이의 거리를 같다고 정의하는 것이 맞을까? (a)에서의 x,y는 서로 outlier 임을 알 수 있으며 (b)에서의 x,y는 평균적인 데이터임을 알 수 있다. 그렇기 때문에 (b)에서는 각각의 점이 평균적인 분포, 즉 기존 데이터의 분포에서 나온 데이터이기 때문에 (a)에서의 outlier 간의 거리보다 더 가깝게 계산되어야 할 필요성이 있다.
위의 예시에서 하나 더 추가해서 설명해보자면 y는 그대로 두고 x를 두 좌표 각각의 중앙에 있다고 생각해보자. (a)에서의 거리는 기존 데이터, outlier 간의 거리이고 (b)에서는 기존 데이터간의 거리이기 때문에 (b)에서의 거리가 더 가깝게 표현될 필요가 있다(물론 분야마다 다르겠지만 데이터 사이언스, OOD detection분야에서는 다르게 표현해야한다).
그렇기 때문에 데이터의 맥락(표준편차, 즉 데이터의 분포가 어떠한지)에 따른 거리 metric이 필요한 것이다.
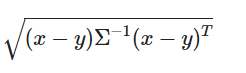
이를 고려한 지표가 마할라노비스 거리이며 나타내보면 위와 같다. 유클라디안 거리와 비교해보면 사이에 공분산 행렬이 들어간 것을 알 수 있으며 공분산 행렬은 각 데이터간의 내적으로 표현된다. 각 데이터간의 내적은 데이터간의 얼마나 닮아있는지 표현할 수 있다(이 부분은 공돌이님의 블로그에서 더 자세히 확인 가능. X행렬에 대해 원시행렬 Z와 선형변환 행렬 R을 이용하여 설명해주시는데 처음에는 조금 어지러울 수 있지만 집중해서 보면 잘 이해 가능).
조금 더 내 분야에 적용시켜 64개의 배치 안에 63개의 ID 데이터가 있고 1개의 OOD데이터가 있으며 각각의 데이터에 대한 score function을 구한다고 할 때(물론 여기서 feature encoder가 해당 OOD 이미지를 ID데이터와 다른 feature vector를 잘 뽑아낼 수 있어야할 거 같다), OOD데이터에 대한 feature vector는 다른 vector와는 조금 다른 공간에 mapping 될 것이고 이에 대한 거리를 구했을 때 더 높은 값이 나와야 할 것이다.
'mathematics' 카테고리의 다른 글
| 베르누이 분포와 Cross entropy (1) | 2023.12.23 |
|---|---|
| Bayes Theorem의 MAP, MLE에 대한 이해 (0) | 2023.12.23 |
| Precision, Recall 구분 및 공부 (0) | 2023.07.21 |
| 베이즈 정리(Bayes' Theorem) 이해하기 (0) | 2023.01.04 |
| 몬테카를로 시뮬레이션이란?(Monte Carlo Simulation) (0) | 2022.11.05 |

