| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- BYOL
- shrinkmatch paper
- ConMatch
- shrinkmatch
- mme paper
- 최린컴퓨터구조
- Meta Pseudo Labels
- dann paper
- remixmatch paper
- 백준 알고리즘
- UnderstandingDeepLearning
- 딥러닝손실함수
- WGAN
- CoMatch
- cifar100-c
- Pseudo Label
- 컴퓨터구조
- adamatch paper
- dcgan
- SSL
- simclrv2
- conjugate pseudo label paper
- CycleGAN
- Entropy Minimization
- CGAN
- GAN
- mocov3
- Pix2Pix
- tent paper
- semi supervised learnin 가정
- Today
- Total
Hello Data
비전공생의 Gradient Descent(경사 하강법)살펴보기 본문
딥러닝 모델을 만지면서 당연히 해왔던 것들인데 기초는 닦아도 닦아도 끝이 없기 때문에
한번 정리하고 넘어가려고 합니다. 사실 이 내용만해도 한 학기 수업을 할 수 있을 정도로 방대하지만
앞으로의 모델을 만지면서 당분간 무리없을 정도로 정리해보려고 합니다.
(사실 우연히 본 영상이 너무 재밌어서 한번 정리하고 넘어가야 할 것 같네요.. 해당 동영상은 여기
Grdient Descent는 경사하강법입니다.
그리고 많은 논문에서 'gradient가 소실되었네' ,'gradient가 없어 학습이 진행이 안되네 '
이러한 문구들을 많이 찾아볼 수 있습니다(최근 논문들을 보면서 더 느끼는 거 같습니다)
그렇다면 이 Gradient Descent는 왜 필요한 걸까요?

예를 들어 MNIST 데이터셋을 통해 숫자들을 구별하는 모델을 만들려할 때 어떻게 학습을 진행시킬까요?
그림의 마지막 output layer를 보면은 10개의 뉴런이 있습니다. 일반적으로 sigmoid라는 함수를 주어 각 뉴런마다
0~1사이의 값을 나타낼 수있도록 하는데 이는 우리가 확률이라고 해석해도 무방할 것입니다.
예를 들어 입력값이 8이 들어온다면 기계들은 뉴런들이 서로 상호작용을 통해 9번째 뉴런의 값이 1이 되도록 해야합니다.
그렇지만 당연하게도 기계들은 input값인 8을 이미지8이 아닌 0~255사이의 픽셀들의 집합으로만 인식하기 때문에
처음에는 1이 아닌 엉뚱한 값을 내놓을 것입니다.

그렇다면 어떻게 기계들은 어떠한 방식으로 학습을 진행시켜야할까요?
한가지 방법이 가장 널리 쓰이는 Gradient Descent 방법입니다.
먼저 학습을 진행시키기 전에 우리는 기계에게 어느 정도 틀렸는지 비용(cost)를 알려줄 필요가 있습니다.
그림1에서의 마지막 뉴런들은 기계가 각각 숫자들을 인식할 확률이라고 하였고, 이를 통해 우리는
만약 9번째 뉴런에서 1이 나와야 하고 나머지 뉴런에서는 0이 나오는 것이 인상적이지만 만약
$(0.1, 0.2, 0.2, 0.5, 0.4, 0.3, 0.7, 0.2, 0.1, 0.5)$ 이렇게 나온다면
$(0-0.1)^2 + (0-0.2)^2 + .. (1-0.1)^2 + (0-0.5)^2 = 5 $ 이렇게 기계한테 방금 한 결과에 대한
비용을 알려줄 수 있습니다.
기계가 할 수 있는 이상적인 비용값은 0일 것입니다. 그렇다면 최소한 다음 학습에는 이전보다는 낮은 비용 값이 나와야합니다.
그것을 이루기 위해 Gradient Descent 방법이 필요한 것입니다.
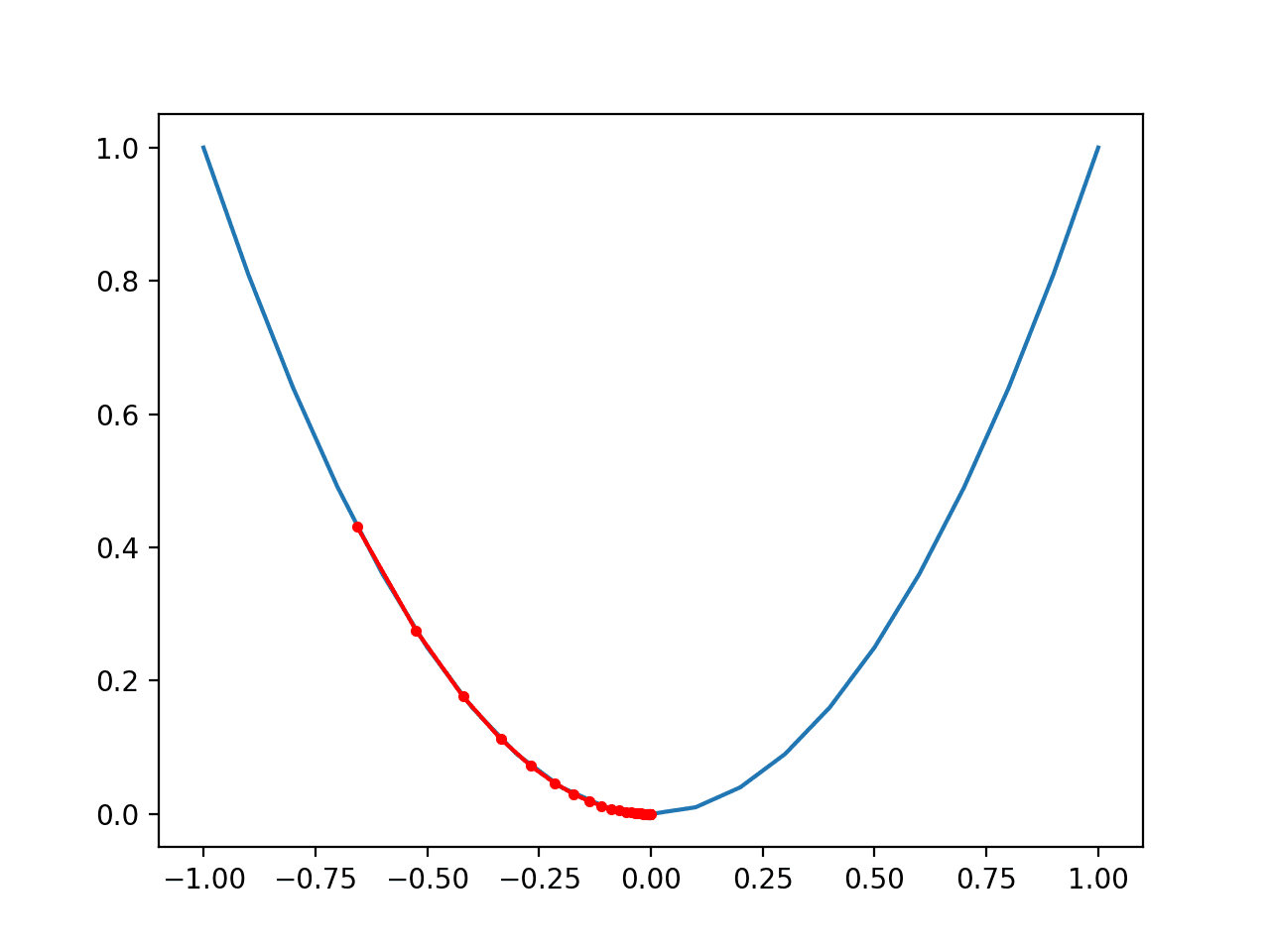
손실함수의 그래프가 그림3과 같다고 했을 때 가장 해당 지점에서의 기울기를 구한 후
기울기가 음수면은 오른쪽으로 이동하고, 기울기가 만약 양수면은 왼쪽으로 이동하는,
한마디로 minumum 값을 향해 가는 알고리즘입니다.
손실 함수에서 해당 x에 대한 gradient 를 계산한다면 $\triangle x $ 는 단위 $x$ 한단위 증가할 때마다 함수 값이 얼마나
증가하는지 나타내고, 또한 방향을 가르키기 때문에 우리는 비용함수의 값을 최소화하는 것이 목적이므로
식을 세운다면 $x = x - \alpha\triangle x$ 가볍게 식을 세울 수 있을 것입니다. 그렇지만 보통 함수가 간단하지 않죠.

상상할 수도 없지만 아마 기계가 마주하는 함수는 이것보다 더 복잡할 것입니다.
그렇다면 우리는 이 복잡한 함수 속에서 minimum 값을 어떻게 찾을까요?
그림1에서의 모델을 보시기만 하더라도 입력값 784, hidden layer 의 10, output의 10개의 뉴런,
만약 가중치들의 개수를 세어본다면 784 * 10 + 10 * 10 + (10 + 10) 총 7960개의 가중치가 있고
그렇다면 아까 장난스럽게 했던 x하나만의 기울기를 고려하는 것이 아닌 총 7,960개 가중치의 gradient를
가중치를 고려해서 업데이트 합니다.
(조금 전 예시에서는 x하나이니 값이라 했지만 여기서는 7,960 차원의 벡터입니다, 또한 엄청나게 많은 양의 가중치들을 gradient를 이용해 업데이트 해주는 방법이 backpropagation이고 이것은 다음에 한번 다루겠습니다.)
그림1을 다시 예로 들면 기계들은 학습을 하는 도중에 어떤 것이 8을 인식하는데 도움이 되는지 계산할 것입니다.
이것도 논리적으로 하는 것이 아니라 학습 과정에서 어떤 뉴런들을 올리고 낮춰야 손실값을 낮출 수 있고
자연스럽게 학습을 통해 알 것 입니다.
그렇다면 기계는 많은 가중치들의 gradient를 계산을 한 후 손실함수를 줄이는 방향으로 나아갈테지만
여기서 local minimum에 빠질 수 있습니다. 기계가 학습과정에서 주변을 둘러보았을 때 현재있는 곳이
손실함수를 최소화해준다고 생각했을 때 학습을 끝마칠 수 있습니다.
그렇기 때문에 손실함수가 매끈한 함수인 것이 중요하다고 합니다.
예를들어 함수 위에서 공을 굴린다고 했을 때 그림3의 함수처럼 군데군데 local minimum들이 많다면,
공은 가장 낮은 곳으로 향하는 곳이 아닌 떨어진 위치에 따라 주변에서 가장 낮은 곳으로 이동할 것입니다.
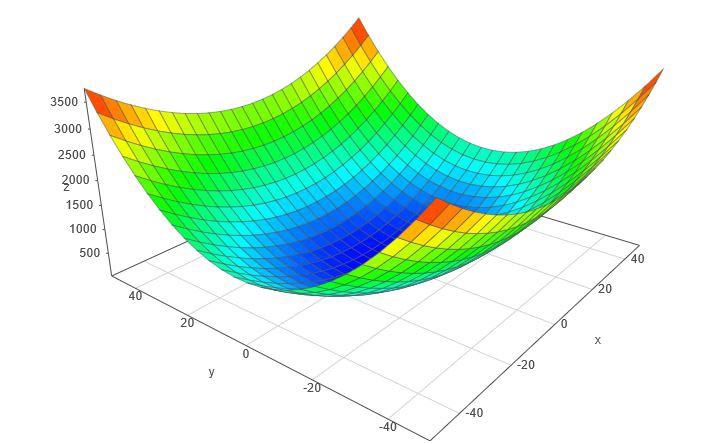
만약 매끈한 함수라면 공이 어디서 떨어지든 최소값으로 잘 수렴할 있을 것입니다.
이 부분에 대해서는 사실 공부하면 할 수록 더 내용이 방대해지기 때문에 여기까지 하겠습니다.
한번 Gradient Descent에 대해서 기계가 학습하는데 어떤 역할을 하는지 가볍게 찾아봤는데요,
평소에 어떻게 레이어를 쌓을지만 고민하고 손실함수는 아무 생각 없이
Cross Entropy를 쓰고 MSE 를 쓰고는 했는데요, 앞으로는 이 부분을 신경쓰면서 모델을 설계해야겠습니다.
틀린 점 지적해주시면 감사하겠습니다.
'딥러닝' 카테고리의 다른 글
| 딥러닝 Momentum(관성)에 대한 이해 (0) | 2022.11.25 |
|---|---|
| 비전공생의 Backpropagation(역전파) 직접 손으로 해보기 (0) | 2022.11.09 |
| ResNet(2015) 구조 리뷰 (0) | 2022.10.25 |
| GoogleNet(2014) 구조 리뷰 (0) | 2022.10.23 |
| VGGNet(2014) 구조 리뷰 (0) | 2022.10.22 |




