| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- WGAN
- semi supervised learnin 가정
- Meta Pseudo Labels
- conjugate pseudo label paper
- Entropy Minimization
- CoMatch
- shrinkmatch
- GAN
- adamatch paper
- UnderstandingDeepLearning
- ConMatch
- dann paper
- cifar100-c
- 백준 알고리즘
- remixmatch paper
- dcgan
- simclrv2
- mocov3
- SSL
- tent paper
- Pseudo Label
- 컴퓨터구조
- shrinkmatch paper
- Pix2Pix
- CGAN
- 최린컴퓨터구조
- mme paper
- 딥러닝손실함수
- CycleGAN
- BYOL
- Today
- Total
Hello Data
Epipolar Geometry 공부해보기 본문
해당 내용은 튀빙겐 대학교의 Andreas Geiger 교수님의 강의와 다크프로그래머님 블로그 포스팅 글을 참고하였습니다. 포스팅 아래에 참조 링크있습니다.
Epipolar Geometry란?
Stereo vision : 사람은 2개의 눈을 통해 이미지를 확보하기 때문에 동일한 매커니즘으로 여러 카메라를 통해 영상을 얻어 3차원 거리 정보를 확보(3d 포인트와 카메라간의 거리). 아래 이미지는 예시

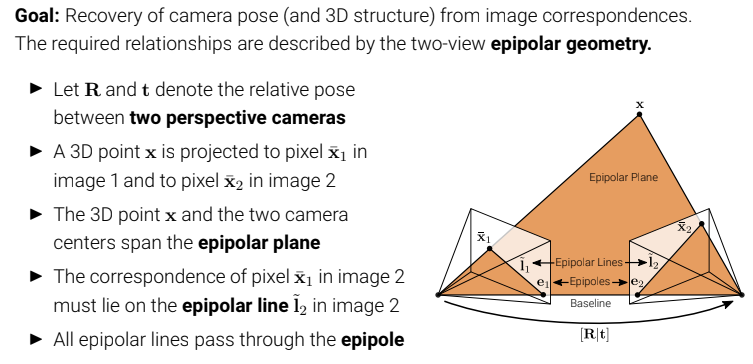
3d 물체를 향해 다른 위치, 다른 각도의 카메라 2대 이상있고 동일 물체에 대해 여러 이미지 평면(image plane)을 획득했을 때, 카메라 포즈 및 3d 이미지 매칭쌍들에 대한기하학적인 관계를 다루는 학문이며 여러 개의 카메라를 동원하여 물체의 입체(깊이)를 얻는 기법인stereo vision을 위해 epipolar geometry를 공부한다고 할 수 있다(각 매칭쌍들에 대한 기하하적인 관계식들을 통해 서로 제약을 주고 깊이를 알아낼 수 있다)
x: 3d point
xbar1: point x를 시점1 카메라에서 얻은 image plane에 정사영한 좌표
xbar2: point x를 시점2 카메라에서 얻은 image plane에 정사영한 좌표
epipolar plane: 3d 물체와 두개의 카메라 원점 좌표들이 이루는 span. 이 span안에 xbar1, xbar2는 존재한다. 그 이유는 3d 좌표인 x는 선형적으로 사영되기 때문인데 더 정확히는 epipolar line에 존재한다고 할 수 있다. 그림에서 잘 확인할 수 있다.
e1, e2: epipole, 각 카메라의 원점을 이은 선과 각 이미지 평면들과의 교점. 그러나 꼭 이미지평면들과의 교점이 아니어도 되고 그럴 경우 infinity한 곳에 있다.
l1, l2: epipolar line, 사영된 좌표와(xbar) 각 이미지 평면들의 epipole를 잇는 선들. 이 선은 epipolar plane과 각 카메라의 이미지 평면이 교차하는 선들이라고 할 수 다.
[R|t] : 시점1 카메라의 원점에서 R만큼 회전하고 t만큼 평행이동했을 때 시점2의 카메라 원점이다.
Q: 각 카메라들의 위치관계를 알고 있고, 왼쪽 카메라의 xbar1 위치를 안다고 했을 때 오른쪽 카메라의 xbar2 위치를 알 수 있을까?
A: 아니오이다. 다음 이미지를 보면 잘 알 수 있다.

3d 물체의 위치가 x1, x2, x3 로 바뀐다고 했을 때 이미지 평면에 투영되는 XR 의 위치는 달라지는 것을 알 수 있으며 각 위치들은 epipolar line에 있는 것을 알 수 있으며 우리가 추가로 알아야 하는 정보는 3d물체와 왼쪽 카메라 원점 위치와의 거리(depth)를 알아야 함을 알 수 있다. 여기서 또 알 수 있는 건 epipolar line은 각 이미지 평면에서 유일하게 존재한다는 것을 알 수 있는다. 이러한 성질을 이용해서 왼쪽 카메라에 대응되는 점을 XL을 이용해서 오른쪽 카메라에 대응되는 epiline을 계산할 수 있는데 이러한 변환관계를 설명해주는 matrix 가 뒤에서 설명할 Essential matrix, Fundamental matrix라고 할 수 있다. 결국 우리는 이러한 matrix들을 활용해서 epiline 에 대한 정보를 및 관계식을 얻어내고 epipole까지 얻어내는 것이 목적이다. 그렇다면 깊이(+위치)는 자연스럽게 도출해낼 수 있다. (ex. 자율주행 자동차, 추적인식, 이상치제거) 위 이미지에서 추가로 알 수 있는건 X의 위치에 따라 epipolar line이 유일한 선이 그어지는 것을 확인할 수 있으며 epipole을 지난다. 추가로 Epipolar geometry는 적은 연산의 비용이 든다.
Q: 결국 우리가 epipolar geometry를 왜 공부하고, Essential matrix를 찾을까?
A: Essential matrix를 한번 찾고 각 카메라의 위치 관계를 안다면 계속해서 epipolar line을 이용하여 3d point에 대하여 위치를 알 수 있다.
Epipolar Geometry
(여기서부터는 수식)
K를 i번째 camera matrix라고 할 때 K ∈ $R^{3x3}$ 라 할 수 있다(x,y,z좌표를 가지는). 그렇다면 xtilda = K^-1 * xbar 라고 할 수 있고 xtilda 는 카메라 i에서의 xbar pixel 에서의 local ray direction이라고 할 수 있다. 다시 한번 설명해보자면 3d 이미지 X, 카메라1 에 의해 이미지 평면에 투영된 xbar에 대해, xbar = K * X 이 성립하는데 양쪽에 K의 역행렬을 곱해주면 K^-1 * xbar = X가 되는데, 여기서 카메라 좌표와 투영된 이미지만으로 깊이(입체)를 알 수 없으니 이는 직선으로 표현된다.

여기서 ∝ 기호는 proportionality를 뜻하는데 x2tilda와 카메라 중점 x2는 반드시 proportional 한 위치에 있다. 그렇다면 x2 와 x1의 calibration을 [R|t] 라 한다면 오른쪽과 같은 식도 proportional함을 알 수 있다(scaling relationship).
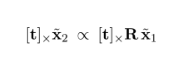
그렇다면 좌변의 xtilda2, 우측의의 R* xtilda1 + (s*t) 에 [t] 를 외적해준다면 위 같은 식을 얻을 수 있다. 여기서 st 가 사라진건 st 에 [t]를 외적해봤자 0이 되기 때문이다.
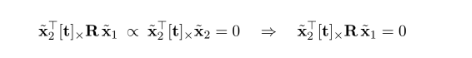
여기서 추가로 xtilda2 전치된 행렬을 양쪽에 내적해보자. 그렇다면 triple product 법칙(내적과 외적의 조합으로 3개의 행렬 or 벡터 연산이 있을 때 2개가 같다면 그 값은 0이다)에 의해 오른쪽 값이 0이 되고 이는 왼쪽 값도 오른쪽 값과 proportional 하기 때문에 0이된다. 여기서 이 식에 대하여 기하학적인 의미를 생각하기 보다는 위에서 설명했던 것처럼 각 점을 대응시키고 찾기 위한 제약식이라고 보면 된다(Epipolar constraint).
여기서 [t| x R을 Essential matrix라고 했을 때 다음과 같은 식을 확인할 수 있는데 이러한 식을 epipolar constraint라고 하며 여기서의 Essential matrix는 항상 존재한다(항상 존재한다는 것에 대한 개인적인 해석: 매칭점이 항상 존재한다). 이 constraint 의 목적은 임의의 두 지점에서 찍은 매칭점들은 이러한 constraint 를 통해 관계 지을 수 있는 것이 핵심이다. E 를 이용해 전개하지 않아도 위의 관계식을 얻을 수 있다는 것을 확인할 수 있다.


추가로 위와 같은 관계식을 얻을 수 있는데, 이것을 기하학적으로 설명해보자면, E * xtilda1 은 왼쪽 카메라에서의 이미지에 대한 3d 좌표를 이와 상응하는 오른쪽 카메라에서의 epipole line을 의미한다. 따라서 다음과 같은 관계식을 추가로 얻는다. 이에 대한 증명: https://edward0im.github.io/mathematics/2020/06/05/multiple-view-geometry2/
해당증명은 E *xtilda1 에 대한 증명이 아니라 E * xbar1 에 대한 증명
위의 관계식에 양변에 e2tilda 를 곱해주면 다음과 같은 식을 얻는다.

해당 식을 만족하는 이유는 epipole 은 항상 epipolar line에 속해있기 때문이다. 그렇다면 동치인 우변도 같이 0이라는 값을 얻게 된다. 이 값이 0인 이유에 대해서는 epipolar line과 epipole에 대해 다음과 같은 평면의 방정식을 만족해 0인 값을 얻은 것 같다.

위의 식에서 x1 tilda의 좌표는 0이 될 수 없고 이는 모든 x1 tilda에 대해서 만족하므로 다음과 같은 식을 추가로 만족한다.
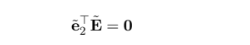
그렇다면 etilda2 는 E 행렬에 대해 0으로만드는 특이값이라고 할 수 있다. 이는 etilda1 역시 해당된다.
Estimating the Epipolar geometry

이 식을 전개해본다면 다음과 같은 식을 얻을 수 있다.

더해지는 각 요소들을 보면은 어떤 요소에는 좌표2개의 내적으로 이루어져 있지만 어떤 요소에는 1개로만 이루어진 곳도 있는데 이러한 것은 노이즈가 불균형하게 증폭될 수 있다(여기서 노이즈라 함은 각 요소를 제한하는 것이 이미지 한개 밖에 없으므로 이미지가 일정 부분 오염된다면 영향이 더 클 것 같다는 의미 같다). 따라서 hartley 가 알아낸 normalized 8 point algorithm(평균0을 가지고 8개의 방정식을 활용)을 적용하면 8쌍의 매칭점들을 통해 E를 구한 후(카메라 파라미터를 알고 있다는 가정) SVD를 사용한다면 이미지를 recover할 수 있다. 8쌍의 알고리즘 외에도 더 적은 매칭쌍들을 이용해 구할 수도 있는데, 각 점들에 대한 constraint를 제외하고도 추가적인 constraint를 가할 수 있기 때문이다.ex) 지면과의 높이 등등

벡터나 행렬에 대하여 ^hat 을 붙이면 그것은 skew symmetric matrix인데, translation vector t를 skew symmetric으로 변환한 것이 t^hat 이다. 여기서 E는 두 카메라의 중심에 대하여 선형변환 정보를 가지고 있는 행렬이기 때문에 특이행렬(singular matrix)라고 할 수 있다(정방행렬 + rank 0이상). 그렇다면 특이값 분해에서 A = U∑V^T 로 나타낼 수 있는데 여기서 A가 E로 들어간다. 여기서 0은 singular value가 0이라는 뜻인데 여기서 특이값 0은 E의 rank가 E의 행 또는 열의 수보다 적다는 것을 의미한다. 여기서 t^hat은 left singular vector를 나타낸다. 그러나 실제 데이터에서는 noise가 난무하기 때문에 singular value가 0이 아닌 경우가 많다고 하는데 0으로 가깝게 하는 것이 좋다고 한다.
fundamental matrix

만약 camera matrix인 K를 모를 경우 local ray direction을 사용할 수 없는데, 대신 이미지 평면 안의 픽셀 좌표인 xbar를 이용할 수 있다. 따라서 xtilda 좌표들을 다 xbar로 바꿔주면 위와 같은 식을 얻을 수 있다. 양 끝의 xbar 픽셀을 제외하고 나머지 부분들을 F(fundamental matrix)라고 할 수 있다(기존 E 에서 camera matrix들이 곱해진 것을 알 수 있다). F를 구하기 위해서는 최소 7쌍의 매칭점들이 필요하다. 여기서 camera matrix를 알 수 없기 때문에 우리는 단순히 perspective reconstruction을 얻을 수밖에 없다.

위와 같은 이미지에서 epipolar line을 확인할 수 있는데 왼쪽에 해당하는 epipolar line, epipole을 안다면, 오른쪽 이미지에 대해서도 epipolar line 을 그을 수 있으며 상응하는 지점에 대한 후보들을 그려볼 수 있다.
Triangulation
위에서 epipolar constraint를 이용해 두 이미지 평면의 기하학적인 관계식을 다 풀어냈다고 하면 3d 이미지에 대한 깊이 및 거리를 정확히 복원할 수 있을까?
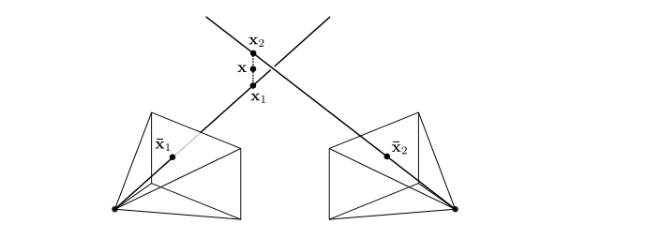
노이즈가 없다면 정확히 가능하지만, 현실은 그러지 않으므로 오차없이는 불가능하다 하며 이 오차를 줄이는 것이 중요한데 이를 위해서 쓰이는 것이 Triangulation이라 할 수 있다.
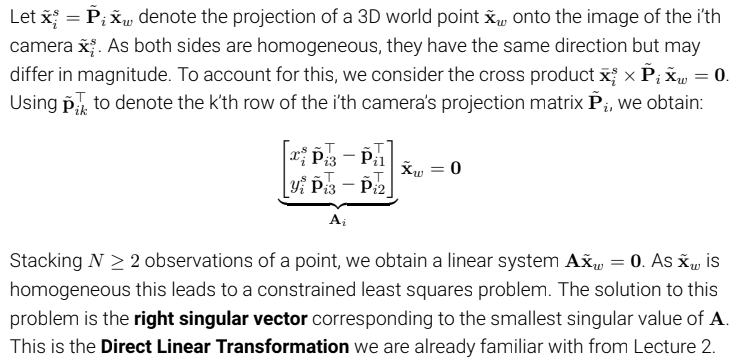
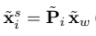

(위에서 xbar x P * xwtilda = 0 이라고 되어있는데 오류이다. 해당 강의영상에서는 xtilda로 되어있다)해당 식들을 하니씩 살펴보면 우변의 xwtilda 는 실제 3d 이미지 포인트를 말한다. P 는 i번째의 카메라 projection matrix를 뜻한다. 좌변은 i 번째 카메라의 이미지 평면에 투영된 homogeneous 좌표를 말한다. epipolar constraint 를 설명할 때 나온 관계식과 형식은 비슷하다. 아마 표기법이 다른 이유는 이전에 K와 이미지 관계식을 풀었기 때문에 그런 것 같다는 개인적인 생각이다. 여기서 양변에 xi tilda를 외적해준다면

이렇게 0이 되는걸 알 수 있는데 그 이유는 xw 에 대해서 어떤 알려지지 않은 scale factor를 곱한 것이 xi 이기 때문에 0 값을 얻을 수 있다. 앞에있는 외적 값을 먼저 계산해주면 다음과 같은 선형 식을 얻게 되는데
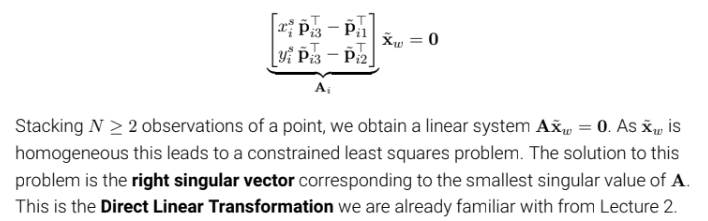
카메라가 2대 이상, 더 많을 경우 더 많은 constraint를 얻을 수 있으니 더 손쉽게 xw 값을 구할 수 있다고 한다. (P는 3차원 matrix이고 xitilda 도 homogeneous 인데 왜 2개의 row만 연산이 되는지 -> 나머지 1개 행은 다른 행dependent해 생략 아래는 전개한 식)


위 이미지에서 xsbar 는 projection된 이미지 평면의 좌표를 말하며, xbar는 augmented vector를 의미한다. xo는 우리가 관찰한 이미지를 뜻하는데 여러 이미지에서 3d point를 근사해 최소값으로 만드는 최적화식이다(gradient based). 아래 이미지를 보면서 비교하면 쉽다(x1bar, x2bar --> xis bar, x --> xw bar, xio --> 계속되는 관찰값) .
Q: 조금 위에서 설명했던 DLT를 사용하지 않고 갑자기 l2 norm을 사용한 이유는?
A: DLT의 결과가 일정하지 않기 때문에 다른 방법을 사용한다고 말한다.

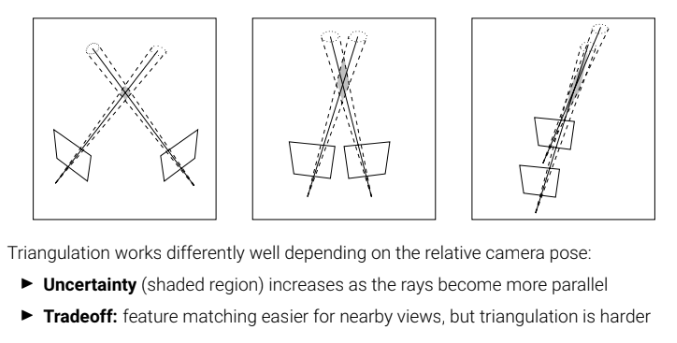
상대적인 카메라들의 위치에 따라서 성능이 좌우된다. 평행할수록 불확실성이 증가한다. 카메라 2개를 이용해서 매칭점들을 구할 때 이 난이도가 쉬울 수록 triangulation의 난이도는 올라간다(카메라가 더 가까울수록).
Orthographic factorization

orthographic factorization은 여러 장의 2d 이미지들을 통해 3차원 이미지를 찾아내는 기술이라고 할 수 있다. i를 frame(사진), p를 feature point라고 정의한다. 첫번째 이미지에서는 한 3d 이미지에 대해 사진을 이용해 두번째 사진처럼 각각의 feature 에 대해 tracking한 것을 알 수 있고, 마지막에 이르러 3d로 복원함을 알 수 있다. 이와 비슷하게 perspective factorization이 있는데 이는 원근감을 더한다고 볼 수 있다.
https://youtube.com/shorts/nuB3f9ks3jI?feature=share

앞으로 진행할 내용에 대한 예시)


그렇다면 위에서 본 3d를 복원하는 건 어떻게 행해질까? xp를 실제의 3d feature라고 했을 때 이미지평면에 (x,y)로 매핑할 수 있는데 여기서 (x,y)는 이미지 평면에서 xp에 대응하는 지점이라고 볼 수 있다. World coordinates에서 i번 째 카메라의 Image coordinates으로의 translation을 t라고 할 때 3d feature에서 t 값을 빼주고 이미지 평면의 기저 벡터들을 각각 곱해줌으로써 이미지 평면을 기준으로 해당 3d포인트에 대한 2d point이미지를 표현할 수 있다.
World coordinates 에서는 이미지의 중심을 원점으로 하고 x,y,z 축을 했을 때 각각 feature들의 합은 0이라고 가정한다.
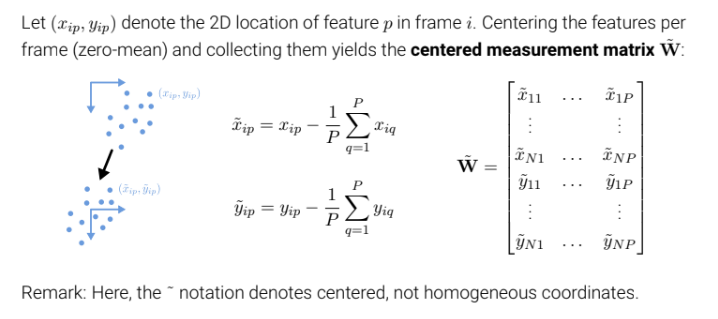
기존의 tilda(물결)가 homogeneous 를 나타냈다면 여기서 tilda는 중심을 뜻한다. 그리고 이전 이미지에서 우리는 실제 좌표계를 이미지 중심으로 잡는다 했는데 몇장의 이미지로는 이 중심을 알아내기 쉽지 않고 이 중심을 알기 위해 노력해야한다. 따라서 (xip, yip)를 observed 된 이미지 feature point라고 한다면 한 사진에서의 여러 관측치들을 이용해 오차를 최소화하여 centering한 결과값이 (xtilda, ytilda)인 것을 확인할 수 있다(world coordinate에서의 중점이 이미지의 중점으로 잡고 feature 들의 합은 0이라고 가정했는데 이를 2d location에서도 적용한 모습같다. 결국 이렇게 업데이트 하는 목적은 각각의 2d 이미지들을 중심을 맞추면 3d 이미지로 복원할 수 있다라고 보는 것 같다).
여기서 행렬 W는 N개의 사진과 P개의 feature point 중심좌표들을 담은 행렬이다.

이전 이미지에서 나온 식을 관계식을 이용해서 전개해본다면 결국 i번째의 p부분 feature point의 중심 x좌표는 이미지 평면에서의 u축과 실제 3d 이미지의 p 부분의 곱으로 나타낼 수 있는데 기존에서 translation한 부분이 없어진 것을 확인할 수 있고 이는 y좌표에서도 똑같이 적용된다.

위에서 얻은 간단한 관계식들은 W = R *X 두 벡터의 내적으로 표현 가능하다(R : i번째 카메라의 unit vector, X : 3d point . 여기서 R이라고 denoting 한 이유는 3d point에 대해 rotation했기 때문).
그리고 R = (2N, 3) 의 차원을 가지는데 그 이유는 각각의 축(변환)들이 3차원 벡터를 가지기 때문이다. X = (3, P) 차원을 가진다. (의문: Rank는 열과 행 중 한쪽만 확인하면 되므로 선형결합을 통해 나온 W의 랭크는 최대가 3임을 알 수 있다.)

의문:(What은 우리가 관찰한 것에 대한 행렬이라고 할 수 있는데 이러한 오차는 SVD를 이용해 줄일 수 있다). 가운데 있는 시그마는 3 Rank를 가지며, R은 left singular vector, X 는 right singular vector를 가지도록 분해할 수 있다. 값을 계속 업데이트 해준다.

그러나 SVD로 분해한 결과는 unique한 결과는 얻지 못하는데, 3차원 Q라는 matrix가 존재하기 때문이다.그렇다면 이 Q를 찾으려면 어떻게 할까? 우선 우리는 위와 같이 3개의 constraint를 얻을 수 있다.
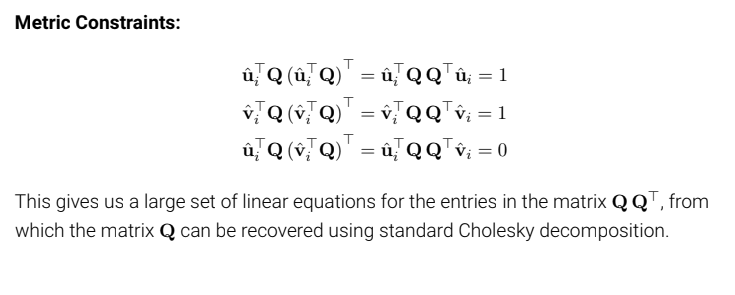
Q 행렬을 식에 추가함으로써 우리는 3개의 제약식을 얻음과 동시에 Q 행렬을 복원할 수 있다. 그 결과 W를 구할 수 있는 X, R을 얻을 수 있다.
장점: 해를 구할 수 있다.
단점: 여러 카메라와 track이 필요하다.
Q: Orthographic factorization에서 보면 모든 카메라가 한 feature에 대해 tracking한 것을 가정한 거 같은데 어떤 카메라가 tracking을 못할 경우에는?
A: 여기서는 모든 카메라가 다 하고 있다고 가정하고 있으며 만약에 하지 못한다면 해당 feature에 대해서는 계산하지 못한다.

여기서 위에서 실행한 단계를 확인할 수 있다.

왼쪽의 frame 2개를 이용해 오른쪽 3d point들을 찾았음을 확인할 수 있으며 이는 1992년에 수행되었다.
https://www.youtube.com/watch?v=nwTVNpF8SMg&list=PL05umP7R6ij35L2MHGzis8AEHz7mg381_&index=9
https://darkpgmr.tistory.com/83
https://en.wikipedia.org/wiki/Epipolar_geometry
'Graphics' 카테고리의 다른 글
| camera calibration 코드 구현 (0) | 2023.06.07 |
|---|---|
| Camera calibration을 위한 여러가지 용어 정리 (0) | 2023.04.13 |


