| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- BYOL
- adamatch paper
- WGAN
- SSL
- UnderstandingDeepLearning
- mocov3
- dcgan
- semi supervised learnin 가정
- 컴퓨터구조
- Pseudo Label
- GAN
- simclrv2
- conjugate pseudo label paper
- 딥러닝손실함수
- CycleGAN
- CoMatch
- ConMatch
- dann paper
- mme paper
- 백준 알고리즘
- 최린컴퓨터구조
- remixmatch paper
- Entropy Minimization
- tent paper
- CGAN
- cifar100-c
- shrinkmatch paper
- shrinkmatch
- Pix2Pix
- Meta Pseudo Labels
- Today
- Total
Hello Computer Vision
Test-Time Adaption via Conjugate Pseudo labels(2022) 논문 리뷰 본문
Test-Time Adaption via Conjugate Pseudo labels(2022) 논문 리뷰
지웅쓰 2024. 2. 11. 01:33해당 논문은 기존의 Tent 논문에서 사용한 Cross Entropy에 대하여 왜 성능이 좋은지에 대해 이론적으로 설명하는 논문이다. 완벽하게 이해하기는 어려웠지만 최대한의 이해를 담았고 조금씩 수정해나가려고한다.
https://arxiv.org/pdf/2207.09640.pdf
Introduction
실제 세계에서의 가능한 모든 distribution shift에 대해서 훈련과정에서 준비하는 것은 불가능하기 때문에, Training 때는 source 데이터로 훈련하고 Test 때는 들어온 input에 대해 잘 adapt토록 하는 것이 Test time Adaption이다(Test Time Training이라고 해도 무방할 거 같다. 세팅에서 약간의 차이는 있을 수 있지만 사소한 거 같다). Test 때 들어오는 데이터는 사실상 unlabeled 데이터이기 때문에 unsupervised objective를 사용해 adaption을 수행해야하며 이것을 TTA loss라고 여기서는 부른다. 그리고 Tent 에서 사용한 TTA loss는 entropy인 것이며 이 entropy 를 최소화하는 것이 목적이었다고 할 수 있다.
저자는 어떠한 TTA를 선정하는가에 있어서 명확하지 않다고 한다(본문에서도 나오지만 대부분의 논문들이 heuristic 하게 사용한다고 언급한다). 따라서 논문에서는 'learn the best TTA loss' 를 하는 것으로 시작했다고 한다. 이것을 meta learning을 통해 수행한다. 그러나 결과적으로 scaled cross entropy를 사용하는 것과 비슷한 결과라고 하며 이 이유에 대해서 convex conjugate를 활용해 이를 설명하려고 노력한다.
Test-time Adaptation via Meta learnt losses
논문의 목적은 TTA에서의 best loss가 어떤 것인지 찾는 것이었고 이를 meta learning을 통해 찾으려는게 저자의 시도였다(meta learning을 위한 파라미터도 따로 있지만 나는 이에 대한 지식이 없어 넘어가려고 한다).
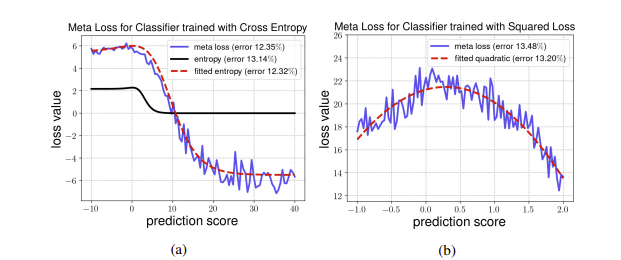
(a) figure를 살펴보면 CE 로 훈련된 classifier에 대해 TTA로 3가지를 실험한 것을 그래프로 나타내었다. 여기서 entropy는 TENT에서 사용한 entropy이고 fitted entropy는 scaling 파라미터를 활용한 entropy라고 보면 된다. 그래프를 보면 이 2개의 plot이 매우 유사함을 알 수 있고 사실상 meta learning에서의 사용되는 loss가 scaled cross entropy아닌가 라는 생각을 저자는 한다(figure b 의 경우도 똑같다고 보면 된다).
Conjugate Pseudo labels
지금까지는 저자들이 meta loss를 통해 발견하려고 했지만 결국 최적의 TTA Loss는 softmax scaled cross entropy였고, 이제 이것이 왜 잘되는지를 증명하는 단계이다. 이를 convex conjugate을 통해 증명하려고 한다.
(최적화 관련 이론들인데 얕게만 이해해보자면 기본적으로 우리가 어느 한 task에 대해 하한점을 찾으려는 primal 문제가 있으면 상한점을 찾는 dual문제도 정의할 수 있는데 일반적으로 이 dual 문제가 더 쉽다고 한다. 완전 독립된 문제가 아니라 primal의 제약식이 dual의 변수였나? 어쨌든 두개의 문제가 연관되어있다, 그리고 계속해서 convex conjugate function이란 말이 나오는데 나는 그냥 dual 문제를 최대화하는 함수구나~ 라고 이해했다)
13-02 Solving the primal via the dual · 모두를 위한 컨벡스 최적화
13-02 Solving the primal via the dual An important consequence of stationarity Strong duality의 조건하에서 Dual solution \(u^{\star}, v^{\star}\)가 주어졌을 때, primal solution \(x^{\star}\)으로 다음의 라그랑지안을 풀 수 있다. \[
convex-optimization-for-all.github.io
아래부터는 Appendix A 에서 나오는 내용들인데 먼저 정리를 하려고 한다.

먼저 h는 logit값을 내뱉는 classifier이며 h(x) 가 축약되었다고 볼 수 있다.
첫번째 줄은 cross entropy를 적은 것이고, 두번째 줄은 이를 분리하고 세번째 줄은 이를 간략화 한 것이다. f라는 함수가 log 확률값들의 합이란 것을 잘 기억하면 된다.
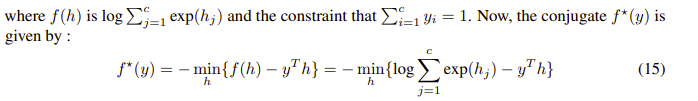
구하기 조금 더 쉬운 Dual 문제로 들어가기 위해 우선 목적함수에 대해 - 부호를 붙여주어 최대화 문제로 바꾼모습이다(개인적인 이해).
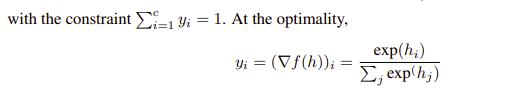
여기서 class 확률 값들에 대한 합은 1이라는 제약이 있다. 그리고 y라는 값에 대해 갑자기 gradient 로 변형하는데 이거는 잘 모르겠다. 이에 대해서는 optimality condition of minimization이라고 하는데, 이를 검색해보면 convex 함수에서의 최적화를 위해서는 도함수 값이 0이라는 것을 나타낸다고 하는데 연결이 되는듯 하면서도 잘 이해가 안간다. 그리고 제일 오른쪽 등식은 여기서 정의한 f(여기서 f는 log probability들의 합을 나타낸다)를 미분하면 오른쪽과 같은 식이 나온다.
(2024.2.17 수정) 여기서 y가 f(h) gradient로 바뀌는 이유에 대해서는 위에서 Cross entrpy: f(h) - y^T * h라고 되있는걸 이항하여 전개한 거 같다
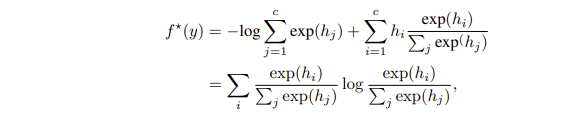
그리고 dual function을 다시 한번 적어보자면 첫번째 줄과 나타낼 수 있는데, 여기서 두번째 줄의 식이 동치라고 하는데 이 부분도 잘 정리가 안되긴한다.
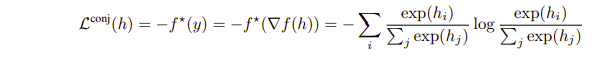
그냥 이해했다고 치고, 결과적으로는 Conjugate loss, 즉 dual function을 최적화한다면 위와 같은 식을 얻게되는 것이다(Appendix 및 4-1,4-2장에 계속 나열되는 식들). 먼저 우리가 최적화하려는 식은 Cross entropy였는데 이를 최적화하는 식이 보니까 Tent 에서 사용하는 entropy minimization이었던 것이다.
여기서 넘어가야할 부분이 $\sum y =1$ 이 gradient 로 표현되는 식인데 그래서 여기 저자는 CPL, 즉 Conjugate Pseudo label을 제시하는데, 알고리즘을 보면 다음과 같다.
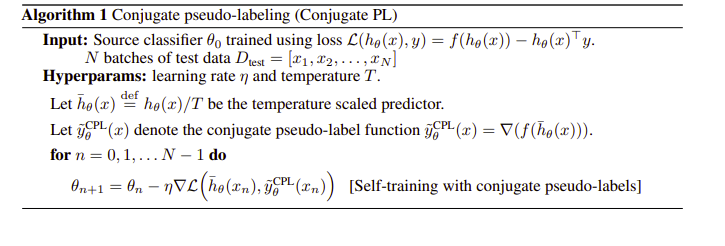
크게 보자면 entropy minimization과 비슷하긴 한데 y label값을 gradient를 이용한 값으로 계산해 약간은 다르다.
(2024.2.17 수정) cross entropy를 사용한 classifier 를 TTT에 사용할 경우 TENT와 똑같은 알고리즘이다. 그러나 이 논문에서는 TENT가 왜 좋은지에 대한 증명을 거치면서 TTT에 사용하는 y값을 재정의하게 되는데 이것이 gradient를 활용한다는 것이다. 이것이 cross entropy를 사용한다면 TENT와 똑같지만 다른 loss를 사용하면 달라진다(이 논문에서는 주로 Poly loss와 비교한다).
Result
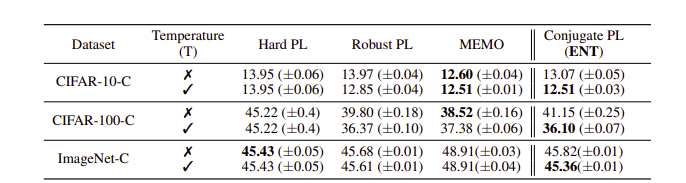
비교한 결과를 보면은 기존의 Tent 에서 사용한 것과 CPL이 큰 차이가 안나긴한다.
(2024.2.17 수정)
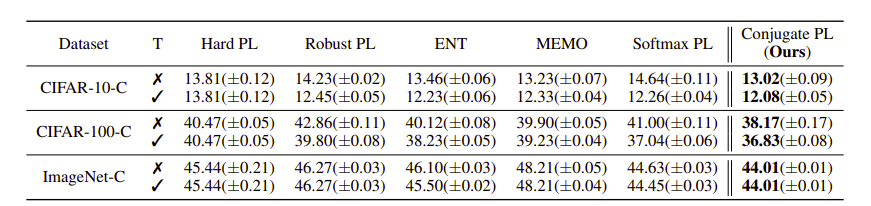
첫번째 table의 경우 cross entropy를 활용한 classifier에 대해 TTT를 수행한 결과라 Conjugate PL 과 Softmax PL, TENT와 같아 비교를 따로 하지 않은 모습이며 아래 table의 경우 Poly loss를 이용한 classifier에 대해 TTT를 수행할 경우 결과가 달라지니 비교를 해주는 모습이다.
많이 어려웠던 논문이지만 우선 이정도만 이해하고 넘어가려고 한다. 틀린 부분이 많이 있지만 아마 계속 수정할 거 같다.



