| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- WGAN
- BYOL
- shrinkmatch paper
- shrinkmatch
- mocov3
- tent paper
- dann paper
- semi supervised learnin 가정
- conjugate pseudo label paper
- Pseudo Label
- CoMatch
- simclrv2
- 딥러닝손실함수
- cifar100-c
- adamatch paper
- 컴퓨터구조
- CycleGAN
- GAN
- mme paper
- ConMatch
- 백준 알고리즘
- UnderstandingDeepLearning
- CGAN
- 최린컴퓨터구조
- dcgan
- Pix2Pix
- SSL
- remixmatch paper
- Entropy Minimization
- Meta Pseudo Labels
- Today
- Total
Hello Data
비전공생의 Test-Time Training with Self-Supervision for Generalization under Distribution Shifts(2020) 논문리뷰 본문
비전공생의 Test-Time Training with Self-Supervision for Generalization under Distribution Shifts(2020) 논문리뷰
지웅쓰 2023. 12. 30. 18:19해당 논문은 TTT라고불리는 Test Time Adation 관련 논문이며 2020년 ICML에서 억셉된 논문이다.
https://arxiv.org/pdf/1909.13231.pdf
Introduction
Supervised learning은 distribution shift에 약하다고 한다. 기존의 Adversarial robustness, Domain Adaption 같은 경우 Training 분포와 Test 분포가 다른 것에 대해 예측(anticipate)하려고 한다. 그러나 저자는 예측을 하는 것이 아니라 Test time에서 배우는 것을 목적으로 한다.
어느 한 Distribution의 unlabeled test데이터가 들어올 경우 우리는 해당 데이터를 통해 test distribution 관련하여 힌트를 얻을 수 있다. 따라서 기존에 방법들처럼 모델 파라미터를 고정시키고 Test시에 이를 예측하는 것이 아닌 Test 시에도 모델 파라미터가 업데이트 된다는 것이다(업데이트 되는 방식은 각 방식마다 다르다. 예를 들어 어느 방법은 각 데이터에 대해서만 업데이트 후 다시 파라미터를 돌리는 경우도 있다)
여기서 사용하는 방법은 Self supervised learning을 활용하여 Test Time Training을 수행하며 이미지를 Rotate 시켜 얼마나 회전 시켰는지를 맞추는 방식을 선택한다. 어떻게 수행하는지는 아래 이미지를 보면 어느 정도 알 수 있다.

Method
Training데이터 $ (x_{1}, y_{1}), ...(x_{n}, y_{n}) $ 가 있을 때 해당 데이터들은 Distribution $ P $에서 나온 데이터들이며 기본적으로 $ min \frac{1}{n} \sum_{i=1}^{n} l_{m}(x_{i}, y_{i}, \theta) $ 를 최소화하는 것이라고 볼 수 있다. 여기에서는 추가적으로 self supervised auxiliary task인 $ l_{s}(x)$를 추가한다. 해당 task 는 $ \theta_{e}$ 를 공유하며 추가적으로 $ \theta_{s} $를 사용한다. main task에서는 따로 $ \theta_{m}$ 을 사용하는 것을 알 수 있으며 위와 같은 구조를 저자는 Y-structure라고 한다. Self-supervised task를 담당하는 branch는 main brainch와 같은 구조를 가지며 단순히 last layer에서의 차원수만 다르다고 한다.
Training 과정에서는 Multi task learning방식으로 훈련이 진행되는데 라벨을 분류하면서도 angle을 맞추게 된다. 이를 수식으로 나타내면 다음과 같다.
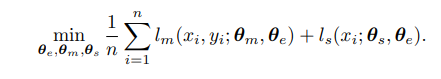
Test Time Training 과정에서는 test sample에 대해서 진행을 한하며 수식을 보면 다음과 같다.
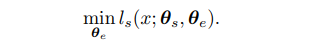
가장 기본적인 부분이니 조금 더 눈여겨 보자면 최소화하는 파라미터는 $ \theta_{e} $ 임을 알 수 있는데 이는 feature extractor이다. 아마 $ \theta_{s} $ 를 따로 하지 않는 이유는 어차피 angle을 잘 맞출 것이니 다른 분포의 이미지가 들어왔을 때 feature extractor만 잘 훈련한다면 잘 하지 않을까? 라는 가정이 있는 거 같기도 하며 뒤에서 언급하기를 두개의 $ \theta $를 업데이트 하나, 하나를 업데이트하나 굉장히 negligible하다고 한다. Test Time에서의 $ \theta_{e}$ 를 최소화 한다면 model은 업데이트된 파라미터들을 이용해 prediction을 하게된다. $ \theta_{x} = (\theta_{e}, \theta_{m}) $.
저자가 말하길 Standard version으로 이 방식을 수행할 때 Test Time시 각 이미지당 update된 $ \theta_{e} $ 는 버려진다고 한다. 즉 업데이트된 파라미터는 버려지고 기존의 Training 시의 파라미터로 돌아가는 것이다. 그러나 만약 Test sample이 Sequential 하게 들어온다면 $ x_{t-1} $ 를 예측하기 위해 업데이트한 $ theta_{e} $ 는 버려지지 않고 $ x_{t}$ 를 예측하기 위해 사용된다고 한다. 이를 Online Test Time Training이라고 말한다.
Empirical results
Test Time Training시에 Batch Norm을 사용하지 않고 Group Normalization을 사용한다고 한다. 그 이유는 배치정규화는 small batch size시에 효율적이지 않다고 하며 이유에 대해서는 batch statistics are not accurate 하다고 한다.
Theoretical Results
여기서는 저자가 소개한 Test-Time Training이 왜 작동할 수 있는지 설명한다. 저자가 발견하기를 Convex model에서 loss function간의 positive gradient correlation을 가지고 있다면 "leads to better performance on the main task after Test-Time Training" 이라고 한다(정확하게 이해가 되지 않아 원문을 실었는데 해석해보자면 여기서 설정한 Auxiliary task를 main task와 잘 설정하면 main task에도 성능이 좋다로 이해하였다).
추가로 이를 입증하기 하기 위해 toy model을 소개한다. regression task(main task)에서의 input x, y가 있고 2 layer network인 A, v가 있다. 이에 대한 loss를 계산하면 아래와 같다.
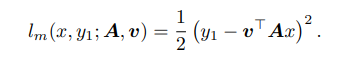
그리고 똑같은 x에 대하여 self-supervised 방법을 수행하기 위해 label $ y_{s}$ 를 만들고 loss를 regression으로 똑같이 설정했을 때 loss는 다음과 같다. 아래에서의 w는 위에서의 v와 역할이 같은데 논문에서의 $ \theta_{s}, \theta_{m}$ 을 담당하고 있다고 보면 된다.
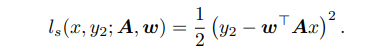
그리고 A(논문 구조에서는 $ \theta_{e}$ ) 를 $ l_{s}$ 만큼 업데이트한다고 하면은 다음과 같이 나타낼 수 있다.
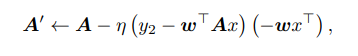
learning rate에 해당하는 hyperparameter를 다시한번 써보면
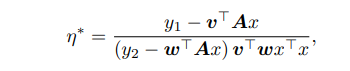
이렇게 될 수 있다는데 따라서 이러한 수식은 main task loss를 0으로 만드는 결과를 가지고 온다고 한다(왜 그런지는 잘 모르겠다). 결과적으로 말하자면 gradient correlationㅇ은 TTT의 중요한 요소라고 한다(model이 convex할 경우)
Result
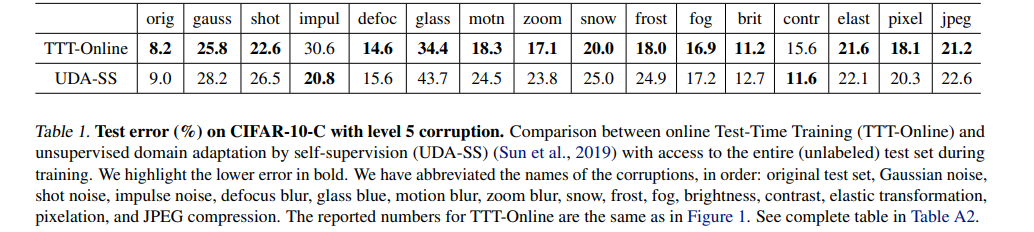
Rotate 방식이 invariant한 이미지에 대해서도 잘 적용될지는 모르겠지만 성능은 좋다고 한다.
'Test Time Adaption' 카테고리의 다른 글
| Test-Time Adaption via Conjugate Pseudo labels(2022) 논문 리뷰 (1) | 2024.02.11 |
|---|---|
| 비전공생의 TENT(Fully Test-Time Adaptation by entropy minimization) 논문리뷰 (0) | 2024.02.07 |
| Test-Time Training with Masked Autoencoders(2022) 논문리뷰 (1) | 2024.01.01 |



