| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- GAN
- CycleGAN
- shrinkmatch paper
- 백준 알고리즘
- 딥러닝손실함수
- SSL
- simclrv2
- Meta Pseudo Labels
- 최린컴퓨터구조
- dann paper
- CoMatch
- UnderstandingDeepLearning
- BYOL
- 컴퓨터구조
- adamatch paper
- conjugate pseudo label paper
- Pseudo Label
- dcgan
- shrinkmatch
- mme paper
- remixmatch paper
- mocov3
- WGAN
- cifar100-c
- Pix2Pix
- Entropy Minimization
- ConMatch
- semi supervised learnin 가정
- tent paper
- CGAN
- Today
- Total
Hello Computer Vision
비전공생의 SimMatch(2022) 논문 리뷰 본문
이번에 읽어볼 논문은 SimMatch이다. 내가 읽었던 논문 중에 손에 꼽힐 정도로 헷갈리면서 오래 걸렸던 논문이다. 그만큼 많은 인사이트를 얻은 거 같다. 이 논문을 읽어보시면 알겠지만 pseudo label을 calibrate하는 과정이 상당히 복잡한데 논문 나온 순서대로 정리하였으며 최대한 제 이해를 담았습니다.
https://arxiv.org/abs/2203.06915
SimMatch: Semi-supervised Learning with Similarity Matching
Learning with few labeled data has been a longstanding problem in the computer vision and machine learning research community. In this paper, we introduced a new semi-supervised learning framework, SimMatch, which simultaneously considers semantic similari
arxiv.org
Introduction
SSL 논문들은 다 그렇듯이 labeled 데이터들은 cost가 많이 든다는 것을 언급한다. 그리고 SSL(semi supervised learning) method들을 통해 대량의 unlabeled 데이터들을 활용하여 performance를 향상시켰다고 말한다.
SSL에서 가장 대표적인 논문은 FixMatch(2020)이다. 여기서는 Pseudo label 방법과 consistency regularization 방법을 활용하는데 어렵지 않아 한번쯤 읽어보는 것을 추천한다.
이 논문에서는 FixMatch에서 나왔던 두가지 방식에 대해 의심을 한다. Pseudo label을 생성하는 것은 완전히 unsupervised 방식인데 이 방식으로 임계값이 넘는다면, argmax 를 취해 label을 취하는 것이 상당히 overconfidence할 수 있다고 말한다. 직관적으로 생각해보면 당연히 모델이 틀린 값을 과대해석할 수 있는 것인데 이것을 믿는 것이 모델의 성능에 안좋은 점이 될 수 있을 거 같다. 그렇기 때문에 여기서는 단순히 semantic (softmax probability)정보만을 활용하는 것이 아니라 similarity(해당 논문에서는 instance level infomration )방법또한 활용을 하며, unlabeled 데이터에 대해 pseudo label을 생성하는 것을 labeled 데이터로 이루어진 memory buffer를 활용하여 신뢰성을 더한다(여기서 memory buffer는 간단히 MoCo에서 나오는 memory queue라고 생각하면 편하다). 추가적으로 기존의 논문들은 label, unlabel 간의 interaction이 없었지만(단순히 label 데이터로 classifier를 훈련하면서 unlabel 데이터들 간의 cross entropy를 사용했다) SimMatch에서는 이 둘을 결합함으로써 pseudo label을 보완했다고 한다.
이 논문의 Contribution 은 다음과 같다.
1. 데이터의 semantic similarity, instance similarity를 활용하는 SimMatch라는 새로운 framework 제안.
2. labeled memory buffer를 활용하여 semantic, instance pseudo label을 aggregate, unfolding technique 방식을 통해 propagate했다.
3. SimMatch framework를 통해 적은 epoch만으로도 SOTA달성.
Method

전체적인 framework는 다음과 같다. 가볍게 설명해보자면 class center는 단순히 softmax probability 값을 뜻한다고 생각하면 된다. 그리고 semantic similarity와 instance similiartiy 이 2가지를 독립적으로 활용하는 것이 아니라 2가지를 결합하는 것을확인할 수 있다. 더 많은 내용들은 밑에서 차례차례 설명하고 있다.
supervised loss는 다음과 같이 정의된다.

B개의 labeled데이터에 대해서는 실제 label값과의 cross entropy를 통해 손실을 계산한다. 나중에 더 많은 표기가 나와서 헷갈리는데 semantic information(probability)는 p로 표현되었음을 알 수 있다.
unsupervised loss는 다음과 같이 정의되어있다.

p위에 있는 w, s는 각각의 feature가 weak augmentation, strong augmentation이 적용된 것을 말한다. 그리고 weak augmentation된 이미지의 argmax 값이 $\tau$를 넘는 unlabel 데이터만 사용한다. 여기서 다른 논문들과 다른 특이한 점은 DA, 즉 Distribution alignment 가 적용된 점이다(물론 ReMixMatch에서도 사용한다).
우선 distribution alignment 에 대해서는 https://arxiv.org/abs/1911.09785 해당 논문에서 distribution alignment 부분만 살펴봐도 충분할 거 같다. 가볍게 설명하자면 MixMatch에서는 entropy minimization을 수행하기 위해서 sharpening 기법을 활용하는데 이 기법은 데이터의 분포가 uniform하지 않는다면 공정하지 않다고 한다. 그렇기 때문에 해당 첨부한 논문에서는 distribution alignment라는 용어를 새로 설정하며 모델의 prediction값을 sensitive으하지 않게 유지하는 것을 목표로 한다.
이것을 다시 말하자면 moving average 를 통해 feature를 보정하는데 사용한다. 여기서 헷갈리는 점은 같은 이미지에 대한 feature를 저장해서 사용하는지이다. 어쨌든 결과적으로 이렇게 moving average를 통해 정규화해준다면 덜 sensitive 하고 reliable할 거 같다는 생각이 든다. 수식으로 보면 다음과 같다.

여기서 DA를 통한 p는 cross entropy를 통해 strong augmentation과의 비교를 통해 loss를 생성한다.
해당 논문에서는 instance similarity matching을 사용하는데 해당 기법을 간단하게 말하면 strong augmentation 데이터와 weak augmentation데이터의 similarity는 같은 값을 가져야한다것이 기본 목적이다(위에서의 semantic은 단순히 classifier를 통한 probability값이고 instance는 MLP를 통해 추출된 vector이다).

논문에서의 similarity함수는 위와 같이 정의한다(어떤 논문에서는 cosine 함수를 사용하고 어떤 논문에서는 내적을 사용하는데 이것을 정하는 기준은 모르겠다).

해당 k는 K개의 memory buffer에서 k번째 feature를 뜻한다. 여기서 memory buffer는 K개의 labeled 데이터들을 모아놓았다(논문에서는 10^5 ++++ memory buffer안에 있는 데이터는 10^5개이며 각각의 데이터는 모두 label 데이터인데, 여기서 각 클래스마다최소 1개의 similarity 를 산출한다고 한다. 예를 들어 총 클래스가 10개라면 최소 10개의 similiary를 산출한다). 그렇다면 분모는 하나의 unlabel data의 weak augmentation 된 이미지와 memory bank안의 similiary 합이고, 분자는 weak augmentation된 이미지와 memory bank에서의 i번째 labeled 데이터와의 similarity이다.그리고 이러한 weak augmentation feature에 대해 similarity를 구했다면 strong augmentation feature 에 대해서도 똑같이 similiarty를 구한다.

그리고 이 2개의 값은 같아야 한다고 위에서 말했는데,

이를 통해 cross entropy를 통해 instance consistency regularization loss를 구한다. 이걸 행렬로 어떻게 효율적으로 계산할지는 모르겠지만 1개의 unlabeled 데이터에 대해 모든 memory bank에 대한 이미지의 similarity를 두 이미지간의 비교를 다 해서 loss를 산출한다면 굉장히 오래걸릴 거 같다는 생각을 한다 >>> buffer안에 있는 모든 데이터를 활용하는 것이 아니다.

그리고 전체적인 loss는 위와 같다.
Label propagation
위에까지만 보면 크게 어려운 점은 없어보인다. 그러나 이 논문에서는 위 pseudo label에 대하여 추가적인 calibration을 가한다. 저자가 말하는 문제점은 위와 같은 방식만 취할 경우 label 데이터를 활용하지 않아 unsuperivsed 방식으로만 활용하는 것이 문제라고 말한다(초기에 언급한 label 데이터와 unlabel데이터 간의 interaction이 없다고 한다). 따라서 labeled 데이터로만 이루어진 memory buffer를 활용하여 labeled 데이터를 최대한 활용하여 pseudo label을 보정한다.
여기서 qw, pw를 따로 보정하기 위해 p_unfold라는 것을 따로 정의한다(추가로 pw 는 L차원이고, qw는 K차원으로 다른 차원을 가진다. 조금 더 생각해보자면 pw는 unsupervised, supervised 에서도 사용되므로 train data의 클래스라고 할 수 있는데 K는 similiarity를 계산한 memory buffer안에서 사용한 데이터 이므로 이 두개의 차이를 두었음을 알 수 있다. 예시로 설명해보자면, pw는 10개의 클래스에 대한 확률 값을 가지고 있다. 그리고 qw는 는 10개의 클래스를 기본적으로 다 가지고 있으면서 첫번째, 두번째 클래스에 대해 추가로 3개의 데이터씩을 더 가지고 있는 벡터라고 볼 수 있다). 여기서 저자가 calibrate하고 싶은 벡터를 qw(anchor이미지와 K개의 similiarty를 가지고 있는 벡터)이다.

많이 헷갈릴 수 있으니 천천히 정의를 해야한다. 우선 qw안에 있는 K차원의 벡터는 각각의 similarity값은 라벨을 가지고 있다(labeled memory buffer안에서 꺼냈기 때문이다). 정의된 $p^{unfold}$ 는 K차원을 가지고 있고, 기존의 classifier를 통해 얻은 pw에서 우리는 anchor가 어디에 속할지에 대한 class확률값을 가지고있다. 다시 한번 위의 수식을 보면은 $p^{unfold}$는 K차원을 가지지만 여기서 similarity를 가지는 것이 아니라 pw에서 측정한 확률 값을 가지게 된다(예시를 들어서 설명해보자면, qw는 [0.8, 0.2] 라는 개 고양이 확률 값을 가지고 있다. 그리고 qw는 [개, 고양이, 고양이, 개라는]대한 similarity로 [0.6, 0.2, 0.3, 0.7] 라는 K차원의 벡터를 가지고 있다. 그렇다면 $p^{unfold}$는 [0.8, 0.2, 0.2, 0.8]라는 K차원의 확률 값을 가지는 것이다) . 조금 복잡했으므로 다시 한번 calibration하는 이유를 살펴보자면, qw에 대한 similarity때문이다. 따라서 단순히 similarity만 사용하는 것이 아니라 classifier에서 예측한 확률 값도 이용하는 것이다. 위의 framework를 보면 이러한 과정이 interaction하는 것을 알 수 있다.
이는 아래와 같이 정의된다. 여기서 class함수는 ground truth 를 return 하는 함수이다. 조금 더 말로 풀어서 이 수식을 설명하자면, i번째 weak augmentation에 대하여 pseudo label을 생성한 후(예를 들어 10개의 클래스가 있다면 각각 10개의 클래스 값에 대한 예측값이 있을 것이다), memory buffer에 속해있는 K개의 개수만큼 p_unfold는dimension크기를 가지며, 각 차원의 값은 memory buffer에 속한 클래스 값을 pseudo label이 예측한 값으로 설정하는 것이다.

위에서 만들어진 p_unfold는 pseudo label p 값에 대해 labeled 정보를 추가로 적용한 것으로 확인할 수 있다. 그리고 이 값을 활용해 q값을 보정한다(이러한 과정에서 similarty는 class값에 대한 정보도 결합하므로 조금 더 reliable할 수 있지만 훈련초기에는 불안정 할 수 있다. 추가로 다른 클래스에 대한 similarity에 대한 값도 올라갈 수 있다 ++ 이렇게 calibration 하는 과정에서 사람이 바라는 점은 similarity, 예측 probability가 둘 다 높고, 아닌 class에 대해서는 둘 다 낮을 경우인데, 이와 반대의 경우가 일어날 수 있기 때문에 성능하락으로 이어질 수 있다 ). 이러한 과정을 거쳐 보정된 q는 아래 식에서 q를 대신한다.

즉 qs는 기존 anchor이미지와 K개의 similarity로만 이루어져있다면 qw는 similarity와 classifier 가 예측한 softmax 확률 값을 추가적으로 결합한 것을 알 수 있다.
q를 보정했으니 이제 보정된 q를 활용해 p를 보정할 차례이다.

위에서 보정된 q값을 구했는데, 이 q값을 활용해 같은 class의 값들을 모두 합한다. 즉 보정된 $q^{w}$는 K개의 데이터에 대한 similarity를 가지고 있는데, 여기서 labeled memory buffer에서 뽑아냈으므로 각각의 클래스를 알고 있다. 따라서 클래스가 같은 유사도 값들을 다 더해주는 것이다.

그리고 이 값과 보정하기 전의 pseudo label값과의 가중치를 통해 새롭게 보정된 p 를 확인할 수 있다.
이러한 과정을 통해 새롭게 보정된 label들을 실제로 loss에 적용하는 것이다. 그리고 이렇게 보정된 label들은 다음과 같은 효과를 가지고 있다.

labeled데이터를 활용해 두 pseudo label을 보정한다면, 두개의 분포가 비슷하다면 이를 더 강화시키며, 다르다면 조금 완화시키는 효과가 있다고 한다.
Memory Buffer
여기서 중요하게 여겨지는 요소가 memory buffer인데, labeled 데이터를 활용하고자 이를 이용하기 때문이다. K개의 데이터와 D차원의 memory buffer Q를 가진다고 하며 label buffer K차원의 데이터를 가진다고 한다. 그리고 위에서 언급한 label propagate 하는 과정에서 memory buffer를 많이 사용하는데 이는 gather, scatter_add function으로 쉽게 이루어질 수 잇다고 한다.
그리고 buffer에 들어가는 데이터의 개수가 많다면 buffer에 들어갈 encoder는 MoCo 처럼 momentum update를 하며, 크지 않다면 단순히 temporal ensemble strategy 를 사용한다고 하는데, 수식은 다음과 같다.
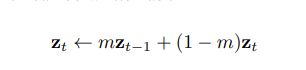
데이터가 많다면 아래의 Student, Teacher network를 사용한다고 한다.

논문에서는 따로 다른 encoder를 사용하지 않고 같은 encoder를 사용했다고 한다.

Result

다른 SSL 방법들과 비교했을 때 우수함을 말해준다.

그리고 논문에서 제안하는 가장 중요한 것은 p, q를 calibration하는 것인데, 이것을 했을 때 성능이 오르는 것을 보여준다.

또한 fixmatch와 비교했을 때 pseudo label의 정확성이 더 높은 것을 확인할 수 있다.
읽을 때 이해가 잘 되지 않았지만 아래 영상을 보고 많은 도움을 받았습니다. 이해가 어느 정도 되니 꽤 재밌게 느꼈습니다.
Reference
https://www.youtube.com/watch?v=5pQa3R59pVY&t=2307s
개인적으로 생각하는 문제점은 K개의 클래스를 뽑는 과정에서 난이도를 고려하지 않았다는 점, labeled 데이터와의 interact를 직접적으로 하는 것이 아니라 labeled 데이터를 활용한 classifier를 활용하는, 간접적이라고 볼 수 있다. 그리고 이 역시 labeled 데이터가 많이 없을 경우 classifier가 잘 훈련이 안됐을텐데 이를 calibration에 활용하는 것인데, 훈련초기의 uncertainty에 대해서 대처점이 따로 없다.
'Self,Semi-supervised learning' 카테고리의 다른 글
| 비전공생의 ConMatch(2022) 논문리뷰 (0) | 2023.08.03 |
|---|---|
| 비전공생의 CCSSL(2022) 논문리뷰 (0) | 2023.08.02 |
| 비전공생의 DASO(2021) 논문 리뷰 (0) | 2023.07.21 |
| 비전공생의 UNet++(2018) 논문 리뷰 (0) | 2023.07.03 |
| 비전공생의 FixMatch(2020) 논문리뷰 (0) | 2023.07.03 |




