| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- GAN
- simclrv2
- dcgan
- BYOL
- dann paper
- WGAN
- CycleGAN
- SSL
- shrinkmatch paper
- 백준 알고리즘
- semi supervised learnin 가정
- 컴퓨터구조
- mocov3
- tent paper
- UnderstandingDeepLearning
- 딥러닝손실함수
- conjugate pseudo label paper
- shrinkmatch
- remixmatch paper
- 최린컴퓨터구조
- adamatch paper
- Pix2Pix
- CoMatch
- Entropy Minimization
- Pseudo Label
- mme paper
- cifar100-c
- ConMatch
- CGAN
- Meta Pseudo Labels
- Today
- Total
Hello Computer Vision
비전공생의 GAN(Generative Adversarial Nets, 2014) 논문 리뷰 본문
GAN에 관심가진지 한 3달 정도가 지났고 논문에 대해서도 한번 겉핥기로 본 적이 있긴한데
앞으로 더 많은 논문을 볼텐데 GAN의 시초인 이 논문을 제대로 안 볼 수 없다고 생각하여
논문을 따로 복사하여 읽었다. 중요한 부분만 소개하는 것보다 논문에서 실린 내용을 최대한 다 소개하려고
노력했다. 코드 구현은 따로 포스팅 할 계획이다.
논문 paper : https://arxiv.org/abs/1406.2661
Generative Adversarial Nets, 즉 줄여서 GAN은 2014년에 이안 굿팰로우에 의해 발표되었다.
1. Introduction
논문을 시작하면서 기존의 generative model들을 소개하면서 장애물들과 단점으로 인하여 어려움이 많았다고 소개한다.
그리고 단순히 marcov chain이 아닌 backpropagation, dropout만을 사용하여 GAN모델을 성공적으로 훈련시킬 수 있다고 말한다. (marcov chain에 대한 언급은 논문 처음부터 끝까지 계속 언급이 된다. 아마 기존 generative model들이 주로 사용한 방법이 marcov chain이 아닐까 싶다.)
adversarial 한 방법을 사용하여 모델을 pit 했다고 소개하는데, counterfeiter(모조범)의 역할을 맡은 generator(G)와 police(경찰)의 역할을 맡은 discriminator(D) 가 경쟁을 통해 학습을 하고, 결국에는 모조범이 만든 작품을 구별하지 못하게 하는 것이 이 논문의 핵심이라고 할 수 있다.

이를 그려보면 다음과 같은데 Discriminator가 두개의 작품을 잘 골라내야하며 이를 헷갈리게 하기 위해
Generator는 진짜 같은 작품을 만들어야한다.
2. Related work
기존의 많은 모델들을 소개해준다.
restricted Boltzmann machines(RBMs), Deep belief networks(DBMs), generative stochastic netwrod(GSN), denoising auto-encoder 등을 소개한다. 그 중에서도 GSN, denosing auto-encoder 방법들을 extend 해서 GAN모델이 나왔다고한다.
3. Adversaral nets
이제 본격적으로 모델에 대한 이야기가 시작된다.

우리가 많은 양의 사람 얼굴데이터를 학습한다면(논문에서는 TFD) 데이터에 대한 확률밀도함수는 다음과 같이 시각화 해볼 수 있다. 해당 그래프를 살펴보자면 데이터셋에는 코의 길이가 40이고 눈의 모양이 50인 데이터가 많이 분포되었음을 알 수 있다. 그리고 이러한 $x$ 의 데이터 분포를 $p_{x}$ 으로 나타내며 generator는 이러한 데이터 분포를 반복적으로 학습하는데 generator 의 분포를 $p_{z}$으로 나타낸다. 이를 기호로 나타내본다면
$$ G(z;\theta_{x})$$ 으로 나타낼 수 있는데 기존 $g$ 의 분포에 대한 파라미터들을 $\theta_{x}$ 라고 했을 때 G라는 함수를 적절하게 학습하여 $p_{x}$ 가 가지고 있는 space에 $z$ 를 올바르게 매핑하는 것이라고 이해하였다.
궁극적인 목표는 $$p_{x} = p_{z}$$ 이며 이러한 목표를 위해 도와주는 것이 $Discriminator(D)$인 것이다.
$D$는 x로부터 왔을 확률로 나타내며 0~1값을 나타낸다.
전체적인 구조를 도식화하면 다음과 같다.
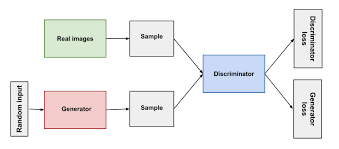
(단순히 G만 훈련하는 것이 아닌 D도 훈련해야하는데 이를 바둑의 예로 들어보자면, 내가 A한테만 바둑을 알려주고 상대 B한테는 알려주지 않는다면, 얼마 가지않아 A는 승률 100%로 항상 이길 것이며 A의 실력도 더 이상 증진되지 않을 것이기 때문에 B도 훈련시키는 것이 중요하다.)
훈련을 위해 $D$는 당연히 $G$가 만든 모조품을 모조품으로 정확히 구별하며 $x$에서 온 것은 진품이라고 구별하는 것이 필요하다. 각각 수식으로 나타내면 $$max(D(x), min(D(G(z))$$ 이며 이를 전체 수식으로 연결해서 나타내보자면
$$min_{G} max_{D} V(D,G) = E_{x~p_{data}}(x) [logD(x)] + E_{z~p_{z}}(z) [log(1-D(G(z))]$$
이러한 수식을 얻게된다. 수식의 왼쪽에서는 $D$ 는 $x$에서 온 것을 진품으로(1) 구별하기 위해 최대화 하려고 하며
오른쪽에서 $G$ 는 모조품을 만들고 이러한 모조품을 $D$가 구분못하게 해야하므로 $log(1-D(G(z)))$ 를 최소화한다.
이를 논문에서는 two player minmax 게임이라고 소개한다.
그리고 이론적인 분석으로는 k steps을 통해 $D$를 훈련 후, 1 step $G$를 훈련한다고 하는데 이는 overfitting을 방지하기 위해서라고 하며 이를 통해 $G$는 천천히 변화한다고 분석했다고 한다.
하지만 실제로는 $G$의 gradient는 충분히 학습하지 못했다고 하며, $D$는 아주 높은 확률로 모조품과 진품을 구분했다고 한다. 이러한 결과로 최소화 해야할 $log(1-D(G(z))$ 가 santurate했다. 라는 표현을 쓴다. 이러한 문제점을 해결하기 위해 $D$를 훈련하기 위해 $D(G(z)))$ 를 최대화하는 훈련을 했다고 한다. 목적은 같지만 이러한 방법이 더 좋은 gradient를 제공했다고 한다.
(직관적으로 한번 생각해보면 처음 $G$가 만든 모조품들은 아주 형편없을 것이며 $D$는 이를 아주 쉽게 구분할 것이다. 그래서 G를 훈련하는 것이 더 어려울 것이라고 생각이 드는데 저자는 이론적으로 D 훈련에 더 치중했다고 나와있다.)
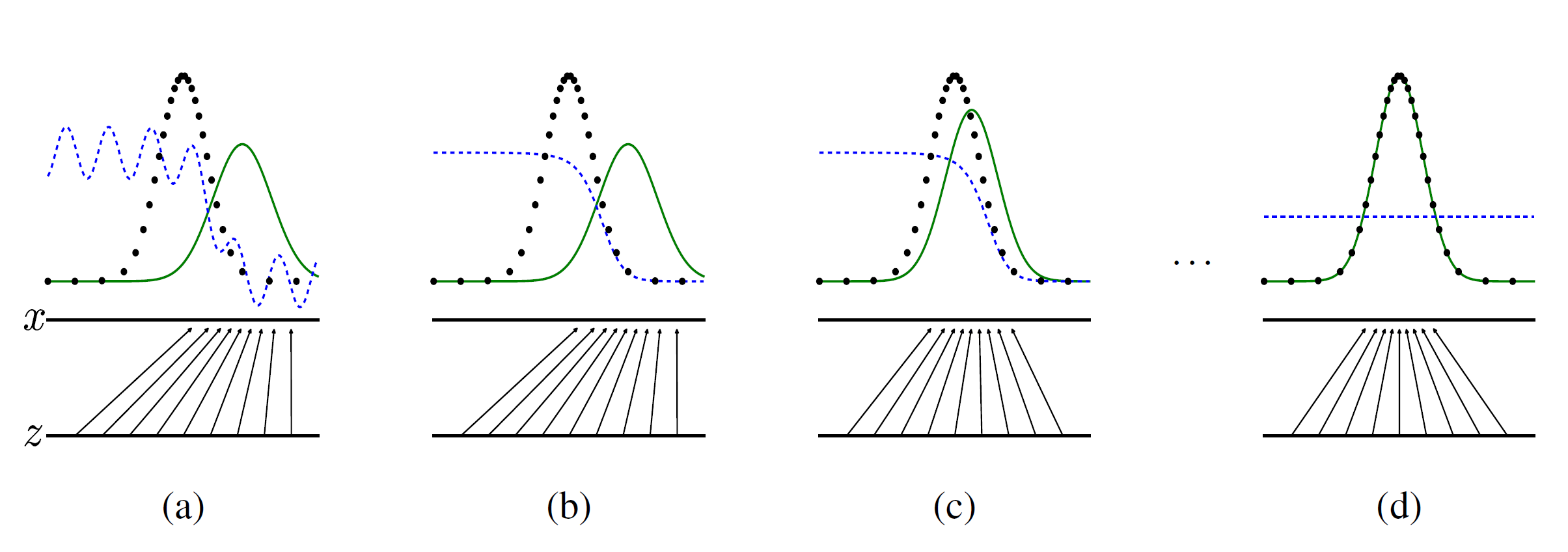
훈련 과정을 시각화한 것이다. 초록색 선은 $p_{z}$의 분포를 나타내며, 파란색 점선은 $D$ 가 구별할 확률을 나타낸다.low horizontal line은 z가 샘플된 것을 나타낸다.시간이 갈 수록 $p_{z}$ 의 분포가 $p_{x}$ 의 분포를 따라감을 확인할 수 있으며 이에 따라 $D$도 수렴하는 것을 알 수 있는데이 값은 $\frac{1}{2}$ 이다. 그 이유는
$$D(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)}$$인데만약 최적으로 수렴한다면 $p_{g} = p_{data}$ 이기 때문이다.
위 식은 D에 관한 미분을 통해 V(D,G) 최대값을 갖는 점을 구하면 $$D(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{g}(x)}$$ 이러한 식을 얻을 수 있다고 한다. (범위는 [0,1])
4. Theoretical Results
여기서는 위에서 언급한 것들을 pseudo code 로 보여준다.
update the discriminator by ascending its stochastic gradient:
$$▽\theta_{d} \frac{1}{m} \sum_{1}^{m}[log D (x^i) + log(1-D(G(z^i))))]$$
k steps discriminator 를 훈련한 후
update the generator by descending its stochastic gradient:
$$▽\theta_{d} \frac{1}{m} \sum_{1}^{m}log(1-D(G(z^i))))$$
이렇게 한 차례 학습이 이루어 지는 것을 확인할 수 있다.
그리고 이 모델에서는 KL divergence를 이용해서 두 분포간의 거리를 수식으로 나타냈는데
$$V(G,D^*) = E_ {x \sim p_ {data} (x)} [ \log(D ^ * (x)) ] + E_ {x \sim p_ {g} (x)} [ \log(1-D ^ * (x)) ]$$
$$ \qquad \qquad \qquad \qquad = E_ {x \sim p_ {data} (x)} [ \frac{p_ {data} (x)}{p_ {data} (x) + p_ {g} (x)} ] + E_ {x \sim p_ {g} (x)} [ \frac{p_ {g} (x)}{p_ {data} (x) + p_ {g} (x)} ] $$
$$ \qquad \qquad \qquad \qquad \quad = - \log(4) + E_ {x \sim p_ {data} (x)} [ \log(p_ {data} (x)) - \log(\frac{p_ {data} (x) + p_ {g} (x)}{2}) ]$$
$$ \qquad \qquad \qquad \quad = - \log(4) + \text{KL} (p_ {data} || \frac{p_ {data} + p_ {g}}{2}) + \text{KL} (p_ {g} || \frac{p_ {data} + p_ {g}}{2}) $$
$$ = - \log(4) + 2 \times \text{JSD}(p_ {data} || p_ {g}) \qquad \qquad$$
이렇게 기존 식을 조금 변경해줌으로써 결국 $G$를 최적화시킨다는 것은 $\text{JSD}(p_ {data} || p_ {g})$를 최소화 시키는 것과 같다고 볼 수 있다.
5.Experiments
모델을 훈련하기 위해 여러가지 데이터셋을 훈련했다고 하는데
훈련 데이터셋은 MNIST, CIFAR10, TFD(Toronto Face Database) 이다.
| Model | MNIST | TFD |
| DBN | 138 +- 2 | 1909 +- 66 |
| Stacked CAE | 121 +- 1.6 | 2110 +- 50 |
| Deep GSN | 214 +- 1.1 | 1890 +- 29 |
| Adversarial nets | 225 +- 2 | 2057 +- 26 |
이렇게 결과를 나타냈고 변동성은 크지만 충분히 매력적인 모델이라고 소개한다.
6. Advantages and disadvantages
마지막으로 장점과 단점을 말해준다.
장점으로는 marcov chain을 사용하지 않고 input 데이터를 직접적으로 건들고 gradient에 사용하는 것이 아니고
discriminator를 통해서 훈련하기 때문에 input의 파라미터가 generator로 copied 되지 않는다고 말한다.
이 뜻은 결국 새로운 이미지를 만들 수 있다는 결과를 의미한다.
단점으로는 Helvetica scenario 라고 하는데 이는 우리가 흔히 mode collapse 라고 한다.
훈련이 완벽하게 끝나지 않았고 새로운 이미지를 만들지 않았는데 discriminator를 속일 수 있는 한가지 이미지만 주구장창
만드는 것을 의미한다. 이는 generative model 에 적합하지 않다.
논문 후기
그래도 저번에 한번 읽은 적도 있었고 vanila GAN 모델이 친숙했기 때문에 읽는데 많은 어려움을 느끼지 않았다.
그렇지만 이렇게 직접 수식을 입력하고 기록하는 것이 머리속으로만 이해하는 것과는 또 다른 느낌이었다.
글로 아는 것을 표현하는 것도 충분히 연습해야겠다는 필요성도 많이 느낀다.
개인적인 첫번째 논문 리뷰이니 정신도 없고 쉽게 풀어 쓰려고했는데 이게 통할지는 모르겠네요..
틀린 점은 언제든 지적해주시면 감사하겠습니다.
코드 구현
https://keepgoingrunner.tistory.com/9
GAN(Generative Adversarial Nets) 코드 구현
지난 번 논문 리뷰에 이어서 코드 구현을 해볼라고 한다. https://keepgoingrunner.tistory.com/8 GAN(Generative Adversarial Nets, 2014) 논문 리뷰 GAN에 관심가진지 한 3달 정도가 지났고 논문에 대해서도 한..
keepgoingrunner.tistory.com




