| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- mme paper
- ConMatch
- dcgan
- simclrv2
- Entropy Minimization
- shrinkmatch
- CycleGAN
- 컴퓨터구조
- conjugate pseudo label paper
- 딥러닝손실함수
- BYOL
- UnderstandingDeepLearning
- semi supervised learnin 가정
- tent paper
- dann paper
- 최린컴퓨터구조
- Pix2Pix
- WGAN
- CGAN
- GAN
- adamatch paper
- SSL
- 백준 알고리즘
- CoMatch
- shrinkmatch paper
- Pseudo Label
- cifar100-c
- mocov3
- Meta Pseudo Labels
- remixmatch paper
- Today
- Total
Hello Data
Probability: Univariate Models 본문
2-1-1. What is probability?
코인 토스에 대한 확률을 말할 때 50%라고 말하기 쉽다. 그러나 확률은 2가지 관점으로 말할 수 있다. 하나는 frequentist 적인 해석이다. 이러한 관점으로 볼 때 확률은 사건에서의 long run frequencies를 나타낸다. 두번째 관점은 Bayesian 으로 보는 것이다. 이러한 관점에서 우리는 확률을 uncertainty 를 수량화할 수 있다. 그러므로 이것은 단순히 반복되는 시도들 보다는 정보들과 근본적으로 연결되어 있다(단순히 frequency 관점으로 보는 것보다 Bayesian 관점으로 보는 것이 더 유용하다는 것을 말하는 거 같다). 예를 들어 우리가 만약 남극의 얼음이 2030년에 다 녹는다는 것을 확률로 생각해보았을 때 이것은 반복적으로 일어날 수 없다. 그럼에도 불구하고 우리는 이러한 불확실성을 해당 사건에 대하여 수량화할 수 있는 것이다. 따라서 이 책에서는 해당 Bayesian 관점을 채택한다.
2-1-2. Types of uncertainty
불확실성은 2가지 이유로 일어날 수 있다. 한가지는 데이터에 대한 우리의 무지로 인한 것이다. 나머지 한개는 내재되어있는 변동성이고 이것은 우리가 줄일 수 없다.
2-1-3-4. Conditional probability of one event given another
여기서 조건부 확률은 다음과 같이 정의한다.

만약 A사건의 확률이 0이라면 불가능한 조건으로는 줄 수 없다.
2-1-3-6. Conditional independence of events
사건들은 흔하게 서로에게 종속적이지만 어쩌면 한 조건으로 인해 독립적인 사건이 될 수 있다. 이를 표기로 나타내면 다음과 같다.

2-2. Random variables
X가 unknown quantity of interest를 나타낸다고 해보자. 만약 X의 값을 모르거나, 변할 수 있을 때 이를 Random variable 혹은 rv라고 한다. 이러한 Random variable이 가능한 집합을 우리는 sample space or state space라고 한다. 예를 들어 X가 주사위에서 나올 수 있는 숫자라고 할 때 {1, 2, 3, 4, 5, 6} 으로 나타낼 수 있다.
2-2-2. Continuous random variables
만약 X가 실수 집합이라면 이를 continuous random variable이라고 한다.
2-2-2-1. Cumulative distribution function
만약 사건 A, B, C 를 $A = (X <= a), B = (X <= b), C = (a < X <= b)$라고 한다면(a < b), 우리는 A와 C의 합집합이 B라는 것을 알 수 있다. 따라서 이를 $Pr(B) = Pr(A) + Pr(C)$ 로 표기할 수 있다. 흔히 우리는 X에 대한 cdf를 다음과 같이 정의한다.

2-2-2-2. Probability density function(pdf)
pdf는 cdf의 미분으로 정의된다.

만약 pdf가 주어진다면 우리는 구간에 대한 확률을 계산할 수 있다.

2-2-3. Sets of related random variables
X, Y라는 rv를 가지고 있다 가정. 이를 X, Y에 대한 joint distribution으로 정의하고 X, Y에 대한 모든 가능한 값에 ㅐ하여 $p(x,y) = P(X = x, Y = y)$로 정의한다. 만약 X, Y를 유한적인 집합으로 나타낼 수 있다면 다음과 같이 표기할 수 있다.

만약 두 변수가 독립적이라면 two marginal의 곱으로 우리는 joint를 나타낼 수 있다. marginal distribution은 다음과 같이 표현할 수 있다.

만약 우리가 possible states Y에 대해 모두 합한다고 할 때 이를 sum rule or rule of total probability라고 한다.
조건부 확률은 다음과 같이 쓸 수 있다.


X, Y가 독립적이면 위와 같이 나타낼 수있는데, 2개 변수에 대한 일반적인 결합 분포를 알기 위해서는 (6-1) * (5-1) = 29 개의 파라미터가 필요하지만 만약 독립적이라면 (6-1) + (5-1)개만 알고있으면 p(x, y)를 정의할 수 있다.
2-2-4. Independence and conditional independence
만약 X, Y가 무조건적인 독립이라면 다음과 같이 나타낼 수 있다.

일반적으로 다음과 같은 표기를 사용할 때 X1, X2, .. Xn은 모두 독립적이라고 말한다.

그러나 무조건적인 독립은 흔치 않은데 그 이유는 많은 변수들이 다른 변수에게 영향을 주기 때문이다. 그러나 주로 이런 영향들은 직결되기 보다는 다른 변수들에 의해 완화되곤 한다. X, Y가 Z로 인한 조건적인 독립은 다음과 같이 나타낸다.

2-2-5. Momments of a distribution
2-2-5-1. Mean of a distribution
분포의 요소 중 가장 흔한 것은 Mean 이며 다음과 같이 나타낼 수 있다.

만약 rv가 이산적일 때는 integral대신 sigma로 나타낸다.
그리고 n개의 rv에 대해 기대값들의 합은 다음과 같이 동치로 나타낼 수있다.

2-2-5-2. Variance of a distribution
분산은 분포의 퍼짐 정도를 나타내고 다음과 같이 나타낼 수 있다.

2-2-5-3. Mode of a distribution
mode는 분포에서 가장 큰 값을 나타내는 것을 말한다.

2-2-5-4. Conditional moments
만약 2개의 rv가 종속적이라고 할 때 우리는 1개가 주어졌을 때 나머지를 계산할 수 있고 이에 대한 증명도 할 수 있다.


2-2-6. Limitations of summary statistics
비록 분포를 평균, 분산, mode로 요약하는건 흔한 일이지만, 이건 정보를 놓칠 수 있다.

위 이미지를 본다면 모두 서로 다른 데이터셋이지만 평균과 분산이 같은 것을 알 수 있다. 그러나 이들의 결합분포, p(x, y)는 다른 것을 알 수 있다. 따라서 더 많은 정보를 얻기 위해서는 box plot, violin plot들을 통해서 알 수 있다.
2-3. Bayes's rule
여기서는 Bayesian inference를 다룬다. inference는 sample 데이터를 지나쳐오면서의 일반화하기 위한 행동이라고 한다. 주로 certainty 정도를 나타낸다. 그렇다면 Bayesian inference는 확실성 정도를 확률을 사용해서 말하는 것이다. 해당 rule은 아주 간단하고 우리가 잘 알고 있다.
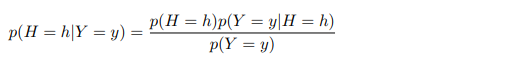
여기서 p(H)는 이전에 어떤 데이터를 보기 전에 우리가 알고 있는 사전분포라고 할 수 있다. p(Y|H = h)는 possible output이라고 할 수 있다. 이를 observation distribution이라고 한다. 우리가 어느 순간에서의 actual observation y를 평가하고 싶을 때 수식은 p(Y = y | H = h)라고 하고 이를 가능도라고 한다. 그리고 P(H = h | Y = y)를 사후 확률(posterior distribution)이라고 한다. 따라서 Bayes rule은 이렇게 나타낼 수있는데,

Bayes rule을 사용해 distribution을 update하는 것을 우리는 Bayesian inference, posterior inference 라고 한다.
2-3-3. Inverse problems
확률 이론은 결과값 y에 대한 분포를 world h가 주어졌을 때 예측하는 것을 관심있어 한다. 반대로 역확률은(inverse probability) y로부터 세상을 아는 것에 관심있다. 이것을 h -> y mapping이라고 한다.
2-4. Bernoulli and binomial distribution
2-4-1. Definition
동전을 던진다고 했을 때 head가 나올 확률은 [0, 1]이다. Y = 1을 head, Y = 0을 tail이라고 했을 때 $p(Y = 1) = \theta $ , $p(Y = 0) = 1 - \theta $로 나타낼 수 있다. 이를 베르누이 분포라고 하고 $ Y ~ Ber(\theta)$ 로 표기한다. 흔히 ~을 쓸 때는 sampled from, is distributed as 의 의미로 사용된다.
2-4-2. Sigmoid(logistic) function
만약 우리가 input x에 대한 이진 변수 y {0, 1} 에 대해 예측하고 싶다면 우리는 조건부 확률 분포를 사용할 수 있다.
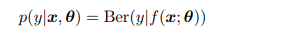
여기서 f는 어떠한 함수이며 [0, 1] 조건을 만족해야한다. 그러나 이러한 조건을 자동으로 만족시키기 위해
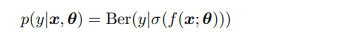
f함수의 결과값에 sigmoid function을 붙여 이를 자동으로 맞추도록 할 수 있다. 이는 주로 확률로 예측이 된다.
2-4-3. Binary logistic regression
여기서 f를 1차 선형식이라고 했을 때 다음과 같이 나타낼 수 있다.

이를 다르게 표현하면 다음과 같이 표현할 수 있다.

이를 logistic regression이라고 한다. 만약 iris dataset에 대해 품종을 virginica / not virginica로 예측한다 했을 때 decision boundary 를 그려볼 수 있다.

2-5. Categorical and multinomal distributions
y의 클래스 집합이 {1,2,..., C}일 때 우리는 categorical distribution을 사용할 수 있다.
2-5-1. Definition
categorical distribution은 클래스에 대한 이산확률분포라고할 수 있다.

2-5-2. Softmax function
조건부 경우에서 우리는 이렇게 정의할 수 있다.
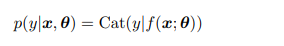
위에서 언급한 것처럼 f에 대한 결과는 [0,1]사이로 정의되야하고 C개의 클래스에 대한 합은 1로 정의되야 하는데 이렇나 조건들을 맞추기 위해서 softmax function을 사용한다.

살펴보면 모든 클래스에대한 출력값에 대해 logit값을 자연상수 지수로 한 합을 분모로 하고 각 클래스에 대한 logit값을 지수로 하는 것을 알 수 있다.여기서 a를 logit이라고 한다.
2-5-4. Log sum-exp trick
흔히 c클래스에대한 확률을 계산할 때 $p_{c} = p(y = c| x) $로 나타낼 수 있다. 또는 다음과 같이도 나타낼 수 있다.

여기서 한 문제를 맞닥뜨릴 수있다. 만약 3개의 클래스가 있고 logit값들을 a = (0, 1, 0) 이면 Z = e^0 + e^1 + e^0 = 4.71인 것을 알 수 있다. 그러나 만약 logit 값이 a = (1000, 1001, 1000)이라면? Z = 거의 무한에 가까운 수인 것이다. 따라서 이러한 문제를 피하기 위해서 log를 사용한다.
2-6. Univariate Gaussian distribution
가장 널리 쓰이는 실수 범위의 분포는 가우시안 분포이고 이를 정규분포라고 한다.
2-6-4. Why is the Gaussian distribution so widely used?
두개의 파라미터(평균, 분산)이 해석하기 쉽다, 중심극한정리에 따르면 독립된 rv는 대략적으로 정규분포를 따른다고 한다.
'머신러닝' 카테고리의 다른 글
| Introduction (0) | 2023.09.10 |
|---|---|
| 머신 러닝 공부 (0) | 2023.09.09 |
| batch size 와 mini-batch size의 차이점 (0) | 2023.04.11 |
| [머신러닝] XGBoost 에 대한 이해 (0) | 2023.02.14 |
| [머신러닝] Gradient Boost 공부해보기 (GBM) (0) | 2023.02.05 |


